Flower 3 — Generalizing experimental findings
Continuing our examination of “the flowers of the First Law” (see previous flowers here and here) this posting looks at one of the most crucial questions in causal inference: “How generalizable are our randomized clinical trials?” Readers of this blog would be delighted to learn that one of our flowers provides an elegant and rather general answer to this question. I will describe this answer in the context of transportability theory, and compare it to the way researchers have attempted to tackle the problem using the language of ignorability. We will see that ignorability-type assumptions are fairly limited, both in their ability to define conditions that permit generalizations, and in our ability to justify them in specific applications.
1. Transportability and Selection Bias
The problem of generalizing experimental findings from the trial sample to the population as a whole, also known as the problem of “sample selection-bias” (Heckman, 1979; Bareinboim et al., 2014), has received wide attention lately, as more researchers come to recognize this bias as a major threat to the validity of experimental findings in both the health sciences (Stuart et al., 2015) and social policy making (Manski, 2013).
Since participation in a randomized trial cannot be mandated, we cannot guarantee that the study population would be the same as the population of interest. For example, the study population may consist of volunteers, who respond to financial and medical incentives offered by pharmaceutical firms or experimental teams, so, the distribution of outcomes in the study may differ substantially from the distribution of outcomes under the policy of interest.
Another impediment to the validity of experimental finding is that the types of individuals in the target population may change over time. For example, as more individuals become eligible for health insurance, the types of individuals seeking services would no longer match the type of individuals that were sampled for the study. A similar change would occur as more individuals become aware of the efficacy of the treatment. The result is an inherent disparity between the target population and the population under study.
The problem of generalizing across disparate populations has received a formal treatment in (Pearl and Bareinboim, 2014) where it was labeled “transportability,” and where necessary and sufficient conditions for valid generalization were established (see also Bareinboim and Pearl, 2013). The problem of selection bias, though it has some unique features, can also be viewed as a nuance of the transportability problem, thus inheriting all the theoretical results established in (Pearl and Bareinboim, 2014) that guarantee valid generalizations. We will describe the two problems side by side and then return to the distinction between the type of assumptions that are needed for enabling generalizations.
The transportability problem concerns two dissimilar populations, Π and Π∗, and requires us to estimate the average causal effect P∗(yx) (explicitly: P∗(yx) ≡ P∗(Y = y|do(X = x)) in the target population Π∗, based on experimental studies conducted on the source population Π. Formally, we assume that all differences between Π and Π∗ can be attributed to a set of factors S that produce disparities between the two, so that P∗(yx) = P(yx|S = 1). The information available to us consists of two parts; first, treatment effects estimated from experimental studies in Π and, second, observational information extracted from both Π and Π∗. The former can be written P(y|do(x),z), where Z is set of covariates measured in the experimental study, and the latters are written P∗(x, y, z) = P (x, y, z|S = 1), and P (x, y, z) respectively. In addition to this information, we are also equipped with a qualitative causal model M, that encodes causal relationships in Π and Π∗, with the help of which we need to identify the query P∗(yx). Mathematically, identification amounts to transforming the query expression
P∗(yx) = P(y|do(x),S = 1)
into a form derivable from the available information ITR, where
ITR = { P(y|do(x),z), P(x,y,z|S = 1), P(x,y,z) }.
The selection bias problem is slightly different. Here the aim is to estimate the average causal effect P(yx) in the Π population, while the experimental information available to us, ISB, comes from a preferentially selected sample, S = 1, and is given by P (y|do(x), z, S = 1). Thus, the selection bias problem calls for transforming the query P(yx) to a form derivable from the information set:
ISB = { P(y|do(x),z,S = 1), P(x,y,z|S = 1), P(x,y,z) }.
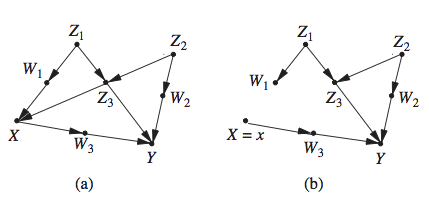
In the Appendix section, we demonstrate how transportability problems and selection bias problems are solved using the transformations described above.
The analysis reported in (Pearl and Bareinboim, 2014) has resulted in an algorithmic criterion (Bareinboim and Pearl, 2013) for deciding whether transportability is feasible and, when confirmed, the algorithm produces an estimand for the desired effects. The algorithm is complete, in the sense that, when it fails, a consistent estimate of the target effect does not exist (unless one strengthens the assumptions encoded in M).
There are several lessons to be learned from this analysis when considering selection bias problems.
1. The graphical criteria that authorize transportability are applicable to selection bias problems as well, provided that the graph structures for the two problems are identical. This means that whenever a selection bias problem is characterizes by a graph for which transportability is feasible, recovery from selection bias is feasible by the same algorithm. (The Appendix demonstrates this correspondence).
2. The graphical criteria for transportability are more involved than the ones usually invoked in testing treatment assignment ignorability (e.g., through the back-door test). They may require several d-separation tests on several sub-graphs. It is utterly unimaginable therefore that such criteria could be managed by unaided human judgment, no matter how ingenious. (See discussions with Guido Imbens regarding computational barriers to graph-free causal inference, click here). Graph avoiders, should reckon with this predicament.
3. In general, problems associated with external validity cannot be handled by balancing disparities between distributions. The same disparity between P (x, y, z) and P∗(x, y, z) may demand different adjustments, depending on the location of S in the causal structure. A simple example of this phenomenon is demonstrated in Fig. 3(b) of (Pearl and Bareinboim, 2014) where a disparity in the average reading ability of two cities requires two different treatments, depending on what causes the disparity. If the disparity emanates from age differences, adjustment is necessary, because age is likely to affect the potential outcomes. If, on the other hand the disparity emanates from differences in educational programs, no adjustment is needed, since education, in itself, does not modify response to treatment. The distinction is made formal and vivid in causal graphs.
4. In many instances, generalizations can be achieved by conditioning on post-treatment variables, an operation that is frowned upon in the potential-outcome framework (Rosenbaum, 2002, pp. 73–74; Rubin, 2004; Sekhon, 2009) but has become extremely useful in graphical analysis. The difference between the conditioning operators used in these two frameworks is echoed in the difference between Qc and Qdo, the two z-specific effects discussed in a previous posting on this blog (link). The latter defines information that is estimable from experimental studies, whereas the former invokes retrospective counterfactual that may or may not be estimable empirically.
In the next Section we will discuss the benefit of leveraging the do-operator in problems concerning generalization.
2. Ignorability versus Admissibility in the Pursuit of Generalization
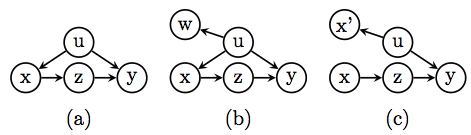
A key assumption in almost all conventional analyses of generalization (from sample-to-population) is S-ignorability, written Yx ⊥ S|Z where Yx is the potential outcome predicated on the intervention X = x, S is a selection indicator (with S = 1 standing for selection into the sample) and Z a set of observed covariates. This condition, sometimes written as a difference Y1 − Y0 ⊥ S|Z, and sometimes as a conjunction {Y1, Y0} ⊥ S|Z, appears in Hotz et al. (2005); Cole and Stuart (2010); Tipton et al. (2014); Hartman et al. (2015), and possibly other researchers committed to potential-outcome analysis. This assumption says: If we succeed in finding a set Z of pre-treatment covariates such that cross-population differences disappear in every stratum Z = z, then the problem can be solved by averaging over those strata. (Lacking a procedure for finding Z, this solution avoids the harder part of the problem and, in this sense, it somewhat borders on the circular. It amounts to saying: If we can solve the problem in every stratum Z = z then the problem is solved; hardly an informative statement.)
In graphical analysis, on the other hand, the problem of generalization has been studied using another condition, labeled S-admissibility (Pearl and Bareinboim, 2014), which is defined by:
P (y|do(x), z) = P (y|do(x), z, s)
or, using counterfactual notation,
P(yx|zx) = P (yx|zx, sx)
It states that in every treatment regime X = x, the observed outcome Y is conditionally independent of the selection mechanism S, given Z, all evaluated at that same treatment regime.
Clearly, S-admissibility coincides with S-ignorability for pre-treatment S and Z; the two notions differ however for treatment-dependent covariates. The Appendix presents scenarios (Fig. 1(a) and (b)) in which post-treatment covariates Z do not satisfy S-ignorability, but satisfy S-admissibility and, thus, enable generalization to take place. We also present scenarios where both S-ignorability and S-admissibility hold and, yet, experimental findings are not generalizable by standard procedures of post-stratification. Rather the correct procedure is uncovered naturally from the graph structure.
One of the reasons that S-admissibility has received greater attention in the graph-based literature is that it has a very simple graphical representation: Z and X should separate Y from S in a mutilated graph, from which all arrows entering X have been removed. Such a graph depicts conditional independencies among observed variables in the population under experimental conditions, i.e., where X is randomized.
In contrast, S-ignorability has not been given a simple graphical interpretation, but it can be verified from either twin networks (Causality, pp. 213-4) or from counterfactually augmented graphs (Causality, p. 341), as we have demonstrated in an earlier posting on this blog (link). Using either representation, it is easy to see that S-ignorability is rarely satisfied in transportability problems in which Z is a post-treatment variable. This is because, whenever S is a proxy to an ancestor of Z, Z cannot separate Yx from S.
The simplest result of both PO and graph-based approaches is the re-calibration or post-stratification formula. It states that, if Z is a set of pre-treatment covariates satisfying S-ignorability (or S-admissibility), then the causal effect in the population at large can be recovered from a selection-biased sample by a simple re-calibration process. Specifically, if P(yx|S = 1,Z = z) is the z-specific probability distribution of Yx in the sample, then the distribution of Yx in the population at large is given by
P(yx) = ∑z P(yx|S = 1,z) P(z) (*)
where P(z) is the probability of Z = z in the target population (where S = 0). Equation (*) follows from S-ignorability by conditioning on z and, adding S = 1 to the conditioning set – a one-line proof. The proof fails however when Z is treatment dependent, because the counterfactual factor P(yx|S = 1,z) is not normally estimable in the experimental study. (See Qc vs. Qdo discussion here).
As noted in (Keiding, 1987) this re-calibration formula goes back to 18th century demographers (Dale, 1777; Tetens, 1786) facing the task of predicting overall mortality (across populations) from age-specific data. Their reasoning was probably as follows: If the source and target populations differ in distribution by a set of attributes Z, then to correct for these differences we need to weight samples by a factor that would restore similarity to the two distributions. Some researchers view Eq. (*) as a version of Horvitz and Thompson (1952) post-stratification method of estimating the mean of a super-population from un-representative stratified samples. The essential difference between survey sampling calibration and the calibration required in Eq. (*) is that the calibrating covariates Z are not just any set by which the distributions differ; they must satisfy the S-ignorability (or admissibility) condition, which is a causal, not a statistical condition. It is not discernible therefore from distributions over observed variables. In other words, the re-calibration formula should depend on disparities between the causal models of the two populations, not merely on distributional disparities. This is demonstrated explicitly in Fig. 4(c) of (Pearl and Bareinboim, 2014), which is also treated in the Appendix (Fig. 1(a)).
While S-ignorability and S-admissibility are both sufficient for re-calibrating pre-treatment covariates Z, S-admissibility goes further and permits generalizations in cases where Z consists of post-treatment covariates. A simple example is the bio-marker model shown in Fig. 4(c) (Example 3) of (Pearl and Bareinboim, 2014), which is also discussed in the Appendix.
Conclusions
1. Many opportunities for generalization are opened up through the use of post-treatment variables. These opportunities remain inaccessible to ignorability-based analysis, partly because S-ignorability does not always hold for such variables but, mainly, because ignorability analysis requires information in the form of z-specific counterfactuals, which is often not estimable from experimental studies.
2. Most of these opportunities have been chartered through the completeness results for transportability (Bareinboim et al., 2014), others can be revealed by simple derivations in do-calculus as shown in the Appendix.
3. There is still the issue of assisting researchers in judging whether S-ignorability (or S-admissibility) is plausible in any given application. Graphs excel in this dimension because graphs match the format in which people store scientific knowledge. Some researchers prefer to do it by direct appeal to intuition; they do so at their own peril.
For references and appendix, click here.