Can DAGs Do the Un-doable?
The following question was sent to us by Igor Mandel:
Separation of variables with zero causal coefficients from others
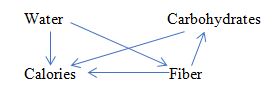
Here is a problem. Imagine, we have a researcher who has some understanding of the particular problem, and this understanding is partly or completely wrong. Can DAG or other (if any) causality theory convincingly establish this fact (that she is wrong)?To be more specific, let’s consider a simple example with kind of undisputable causal variables (described in details in https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2984045 ). One wants to estimate, how different food’s ingredients affect the energy (in calories) containing in different types of food. She takes many samples and measures different things. But she doesn’t know about existence of the fats and proteins – yet she knows, that there are carbohydrates, water and fiber. She builds a respective DAG, how she feels it should be:
From our (i.e. educated people of 21st century) standpoint the arrows from Fiber and Water to Calories have zero coefficients. But since data bear significant correlations between Calories, Water and Fiber – any regression estimates would show non-zero values for these coefficients. Is there way to say, that these non-zero values are wrong, not just quantitatively, but kind of qualitatively?
Even brighter example of what is often called “spurious correlation”. It was “statistically proven” almost 20 years ago, that storks deliver babies ( http://robertmatthews.org/wp-content/uploads/2016/03/RM-storks-paper.pdf ) – while many women still believe they do not. How to reconvince those statistically ignorant women? Or – how to strengthen their naïve, but statistically not confirmed beliefs, just looking at the data and not asking them for some babies related details? What kind of DAG may help?
My Response
This question, in a variety of settings, has been asked by readers of this blog since the beginning of the Causal Revolution. The idea that new tools are now available that can handle causal problems free of statistical dogmas has encouraged thousands of researchers to ask: Can you do this, or can you do that? The answers to such questions are often trivial, and can be obtained directly from the logic of causal inference, without the details of the question. I am not surprised however that such questions surface again, in 2018, since the foundations of causal inference are rarely emphasized in the technical literature, so they tend to be forgotten.
I will answer Igor’s question as a student of modern logic of causation.
1. Can a DAG distinguish variables with zero causal effects (on Y) from those having non-zero effects.
Of course not, no method in the world can do that without further assumption. Here is why:
The question above concerns causal relations. We know from first principle that no causal query can be answered from data alone, without causal information that lies outside the data.
QED
[It does not matter if your query is quantitative or qualitative, if you address it to a story or to a graph. Every causal query needs causal assumptions. No causes in – no causes out (N. Cartwright)]
2. Can DAG-based methods do anything more than just quit with failure?
Of course they can.
2.1 First notice that the distinction between having or not having causal effect is a property of nature, (or the data generating process), not of the model that you postulate. We can therefore ignore the diagram that Igor describes above. Now, in addition to quitting for lack of information, DAG-based methods would tell you: “If you can give me some causal information, however qualitative, I will tell you if it is sufficient or not for answering your query.” I hope readers would agree with me that this kind of an answer, though weaker than the one expected by the naïve inquirer, is much more informative than just quitting in despair.
2.2 Note also that postulating a whimsical model like the one described by Igor above has no bearing on the answer. To do anything useful in causal inference we need to start with a model of reality, not with a model drawn by a confused researcher, for whom an arrow is nothing more than “data bears significant correlation” or “regression estimates show non-zero values.”
2.3 Once you start with a postulated model of reality, DAG-based methods can be very helpful. For example, they can take your postulated model and determine which of the arrows in the model should have a zero coefficient attached to it, which should have a non-zero coefficient attached to it, and which would remain undecided till the end of time.
2.4 Moreover, assume reality is governed by model M1 and you postulate model M2, different from M1. DAG-based methods can tell you which causal query you will answer correctly and which you will
answer incorrectly. (see section 4.3 of http://ftp.cs.ucla.edu/pub/stat_ser/r459-reprint-errata.pdf ). This is nice, because it offers us a kind of sensitivity analysis: how far should reality be from your assumed model before you will start making mistakes?
2.5 Finally, DAG-based methods identify for us the testable implication of our model, so that we can test models for compatibility with data.
I am glad Igor raised the question that he did. There is a tendency to forget fundamentals, and it is healthy to rehearse them periodically.
– Judea
“On two occasions I have been asked [by members of Parliament], ‘Pray, Mr. Babbage, if you put into the machine wrong figures, will the right answers come out?’ I am not able rightly to apprehend the kind of confusion of ideas that could provoke such a question.”
(http://www-history.mcs.st-andrews.ac.uk/Quotations/Babbage.html)
Comment by retlav — January 24, 2018 @ 1:17 pm
Dear Judea, I really appreciate your detailed answer, which, as it turned out, was asked by novices like me from the outset of the Great Causal Revolution. Yet it begs some further comments.
1. “no causal query can be answered from data alone, without causal information that lies outside the data”. Completely agree. But the whole problem is that this causal information is exactly what is unknown and could be only hypothesized. It creates a vicious circle: if one has a wrong causal model in her mind (for whatever reasons) and data then (wrongly) confirm it – what is the right way to get out of it? In the food example the researcher had genuine feeling that water contains calories – and, voila, data just “confirmed” the idea, yielding the non-zero coefficient. This is a very typical situation. Hundreds of models I saw in my life as a researcher and reviewer have this nature. Isn’t it the duty of science to separate those fake causes from the true ones – and do that looking at the data, for there is no other way around? Similarly to what is going on now in inferential statistics – the Great Anti p-value Revolution (http://ww2.amstat.org/meetings/ssi/2017/callforpapers.cfm) – don’t you expect that request for separation of the real causes from all others, if not answered properly, would trigger the Counter Causal Revolution soon, since you like the term? And it seems, it is already started on a very large scale: the whole machine learning, especially its deep learning breed, are completely non-causal, for good or for bad. It’s too big an issue to discuss here, but nevertheless it is exactly right.
2. “the distinction between having or not having causal effect is a property of nature, (or the data generating process), not of the model that you postulate. We can therefore ignore the diagram that Igor describes above”. It sounds weird. Of course, causes are in nature, not in our heads. But, still, why dismiss my poor diagram? Just because you know it is wrong? But if you don’t, would you dismiss it anyway? Based on what? Nature is, as always, silent and doesn’t whisper in one’s ear “Dismiss the diagram, I’m designed differently”. Again, this is exactly the original question – how to conclude it is wrong just looking at the data. It can perfectly be correct, too – who knows in advance?
3. Your other comments seem to reproduce the same circle “if causal model is relevant to nature – the DAG theory is useful”, without considering “if causal model is irrelevant to nature – DAG is useful, because it doesn’t recognize, that model is irrelevant”: “If you can give me some causal information, however qualitative, I will tell you if it is sufficient or not for answering your query” (someone else should decide it is causal information or not); “To do anything useful in causal inference we need to start with a model of reality, not with a model drawn by a confused researcher” (alas, we all confused, especially now, with thousands of variables in big data); “DAG-based methods … can take your postulated model and determine which of the arrows in the model should have a zero coefficient attached to I”t (again – “postulated”. My diagram was also postulated) and other similar statements.
4. In comparison of the “postulated” models in your example from O. Duncan’s book (where author in 1975 raised actually the same question as I’m doing now) you consider different admissible models and based on that make decision about “salvage” of the coefficients on the wrongly specified model. The formulation of the problem is perfect. You correctly explained why O. Duncan is wrong, but your criteria for admissibility will very often fail as well. Imagine the situation which is much simpler than depicted on the first “whimsical” diagram, namely:
This type of diagrams is overwhelmingly popular in science in general and in statistics in particular (the whole huge branch of regression is about those). Any models are admissible in this setting – with all three variables, with each pair and with each separate one. And how to distinguish good from bad? In the article mentioned in a post (https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2984045) I showed how drastically everything is changed in models like that depending on specification only – and with actual variables, not the artificial ones! No salvage foreseen by admissibility.
5. Now, to the main point:
“Can a DAG distinguish variables with zero causal effects (on Y) from those having non-zero effects. Of course not, no method in the world can do that without further assumption.”
It’s hard to say, what kind of assumption is mentioned here (if “about nature” – it was discussed above). It is also hard to say, how good this indeed fundamental problem could be solved (if ever), but I still would not be that categorical; at least some attempts have been made. Two of them (one for binary and another for numerical variables) are described in my article referred above (they both need additional exploration). Another approach to the similar (not exactly that) problem (how to detect automatically direction of the causal relation – and by that reason how to distinguish causal vs correlational relations, at least in principle) is developed by B. Schölkopf and others (http://ml.dcs.shef.ac.uk/masamb/schoelkopf.pdf). DAG theory, impregnated by different criteria of “distinguishability” of fakes and real causes, when (and if) they will be efficient enough, will be able to bear much healthier babies.
6. My personal feeling is, however, that even that is not sufficient: a pure statistical understanding of the complex causal relationship just from the data, in a strong and universal sense, is impossible (and at that point, I’m completely with you). But a remedy would be not the updated versions of the DAG (or any other theory, like potential outcomes), but imitational (agent-based and other) models, where internal logic of causal mechanisms will be organically combined with some statistical learning techniques. A discussion of that though goes far beyond the original question.
Comment by Igor Mandel — January 25, 2018 @ 5:26 pm
I just realize that a diagram I refer to in a text after words “diagram, namely:” (before the only blank line) is not shown because this window does not accept any graphics (or I don’t know how to deal with it). The diagram is very simple: three arrows from Water, Carbs, and Fiber direct to Calories (no mutual relations between the three). Sorry for this inconvenience.
Comment by Igor Mandel — January 25, 2018 @ 6:14 pm
Dear Igor,
Back to the main point: “Can a DAG distinguish variables with zero causal effects (on Y) from those having non-zero effects. Of course not. no method in the world can do that without further assumption.” “It’s hard to say, ….”
I believe this is the source of our disconnect. It is actually NOT HARD to say. And the answer is plain NO; no if, no but, nor “Its hard to say etc etc.” but plain NO. I tried to explain why, writing:
But evidently my explanation was taken as a handwaving argument, not as a logical truth. So here is a hard proof.
Suppose you invent some criterion, CR, that distinguishes X->Y from X<-Y and, based on CR, you decide that X has a causal influence on Y. i.e., the arrow X<-Y is wrong. I will now construct a causal model containing the arrow X<-Y and a bunch of latent variables Z, that matches your data perfectly. I know that I can do it, because if the model's graph (on X, Y and Z) is a complete graph, we know that we can tweak the parameters of the graphs in such a way that it will perfectly fit EVERY joint probability function P(X,Y,Z), and certainly every observed marginal of P, like P(X,Y). This means that no criterion based on P(X, Y) is capable of distinguishing the model containing X->Y from the one containing X<-Y. Hence, if you have such a criterion, it must be based on information NOT in P(X,Y). QED True, many decent researchers who accept "correlation does not imply causation" have not yet internalized the crispness and generality of Cartwright's mantra: "No causes in - no causes out". From your hesitations: "it is hard to say, ... It is also hard to say... I still would not be that categorical; at least some attempts have been made..." I conclude that you are not convinced that the indistinguishability barrier is so tall and so impenetrable. Well, I would invite you then to articulate carefully the criterion that you use in your linked article (which I could not parse) and apply it to the link X---->Y, and I can promise
you that I will find your criterion contaminated with some causal information, however mild and/or obscured.
The same happened in the case of faithfulness, which is a mild causal assumption, but still causal. The same is true for Scholkopf assumptions of additive noise or non-Gaussian noise. These
assumptions are imposed on the generative model, hence they are causal.
I now have the feeling that you (or perhaps others) would like to ask me: How do we distinguish between statistical and causal assumptions. Fortunately, we have a crisp Chinese Wall between the two, so we cannot be blamed for ambiguity or, God forbid, hand waving.
Many prominent and highly revered statisticians fumbled on this point. Some claimed that “Confounding” is a well defined statistical concepts. Others were ready to prove to me that randomization”, “instrumental variables” and so forth “have clear statistical definitions”. [Causality pp. 387-388]. I stopped getting these proposals in the past 15 years, after asking the proposers to express their definitions in terms of joint distribution of observed variables. But perhaps the time is ripe for another rehearsal. I am ready.
If you still believe that you have an assumption-free criterion for telling “a variable with zero causal effects (on Y) from those having non-zero effects”, please post it on this blog, and try to express it in terms of the joint distribution of observed variables.
Judea
Comment by Judea Pearl — January 27, 2018 @ 9:03 am
Dear Judea, thanks a lot for the very detailed answer. It helped a lot, as you may see from my comment.
Let me clarify a bit my position about the distinction between two types of variables.
Let assume, we have X1 and X2, both numerical, and have also some Y=bX1 + R, where R is some unknown (not associated with any X) source for Y values. I would call b “a generative” parameter, in a sense, that via b any value of X generates the certain value of Y (1 g of carbs in a food example generates 4 calories, b=4. R, in this case, would be whatever values dictated by unobserved fats and protein; I would ignore measurement errors). X2, in turn, generates nothing, but it is correlated with Y (for whatever reasons). Parameter b, in common language, could be also called “causal”, but I would not discuss here the difference between causal and generative (I did in the article).
If we make regression estimation of the influence of X1 and X2 to Y, we’ll have Y` = b`X1 + c`X2, where Y` is an approximation of Y, b` – estimation of the real b, and c` – estimation of the real 0. The problem is: could we say, that b` estimates (whatever badly) the real b, but c` estimates (whatever good) just a zero? The difference between the two is fundamental – one generates Y, another – not, while estimates b` and c` could be both very misleading (or not).
In the article, different heuristic criteria for distinction were proposed. On many types of generated data, they distinguished coefficients like b` from those like c` successfully, but not with 100% accuracy. Fig. 15 there (which, unfortunately, I can’t technically reproduce here) shows clearly that some statistics behave very differently for b` and c`. All that is in a process of further verification and doesn’t seem hopeless. I would not be surprised if more strong formal criteria for distinction will be proposed.
And here, it looks, the main point is. You consider conditional probability like P(X, Y) as the main enemy of causality (as a representative of the damned statistical paradigm, etc., to be overcome). And, indeed, it is a huge and almost unpenetrable by alien ideas body, what your struggle for the last 30 years has shown clearly. But my modest food example (and countless other similar things) is not about P(X, Y). It is about Y being generated (in a rough physical sense) by X. In a certain sense, it is a literal (“All too literal”, as Nietzsche would say) interpretation of regression: if b stands for the link between X and Y, in each Y should be “a piece” born due to X, equal to bX (of course, this piece could be random, like in special regressions with random individualised coefficients). It looks like we address different things in a sense. But I recognize perfectly that this generative approach IS NOT the only interpretation of causality – and this is a reason, why I don’t believe, exactly like you, in a possibility of all-embracing causality theory based on data only. So, for the narrow class of causality-related problems (generative-like) I may expect the progress, but in general – no, unless another (imitational) paradigm will be fully applied.
Comment by Igor Mandel — January 27, 2018 @ 5:13 pm
Dear Igor,
I have a hard time understanding your proposal. So I will let other readers respond, if they can.
My main problem are sentences such as: “If we make regression estimation of the influence of S1 and X2 to Y”
I dont know of any method that can do that. What you probably mean is: If we thoughtlessly substitute the regression of Y on X2 for b , then….
But then, why do we need both X2 and X1 ? Why not just say : I have invented a method that distinguishes b = 0 from b > 0.
You seem to be claiming to have found such a method, and that it requires no extra information beside the data.
I can’t follow your referred paper, sorry, but this blog is wide open for you to expose your method in the language of modern causal inference, namely, the language or input-output, or assumptions–to-conclusions. It is an extremely effective language, so it should not take more than 3 sentences to convey the essential ideas
Friendly advice: When you describe your method, do not comment on other people’s works; it breaks the flow of logic. Focus on your proposal, and leave others to a later discussion.
Judea
Comment by Judea Pearl — January 28, 2018 @ 3:59 am
Dear Judea, thanks for this advice. I guess the best way to do it is to finish the simulation experiments and report the results. The only hard thing is – I don’t know how to insert the graphs into a post (copy-paste doesn’t work). And again – many thanks for this thoughtful discussion.
Igor
Comment by Igor Mandel — January 28, 2018 @ 2:38 pm
This a comment to all friends in causal research who are struggling to embrace newcomers into the fold.This discussion taught me that, in addition to internalizing the generality of the “No causes in, No causes out” barrier, people outside the fold also have hard time understanding why we struggle so hard to reach an estimand in terms of the joint distribution. For some people, the joint distribution is a fiction of mathematical probabilists and carries no bearing on practical problems.
It would take some time to explain to them that if we fail to express our query in a form of a probabilistic
estimand, we can forget about estimating it from data.
[In other words, if we cannot estimate our query from an infinite sample, we surely cannot estimate it from finite samples].
It is axiomatic to us, true, but not all researchers come to the problem with the same background.
Judea
Comment by Judea Pearl — January 29, 2018 @ 9:26 am
Igor,
Causal discovery algorithms are a big part of structural causal models/DAG literature, you can get started on it on Judea’s book itself — Chapter 2 of Causality.
The point here is just that any algorithm of causal discovery *must* impose *causal assumptions*.
Just a correction about your understanding of Scholkopf et al — their work *is* grounded on the DAG/SCM framework, you can check their new book below (with free download):
https://mitpress.mit.edu/books/elements-causal-inference
Best, Carlos
Best, Carlos
Comment by Carlos — February 17, 2018 @ 1:45 am
Thanks, Carlos, I’ll be working on it.
Igor
Comment by Igor Mandel — February 27, 2018 @ 2:15 pm
Thanks for your great blog
Could you explain me how to form a DAG of a negative expression?
like in “A=B*-C+B*-C”
how will “-C” be represented?
Comment by bitcohen — March 1, 2018 @ 3:08 pm
Hi all,
I don’t know how to add a separate post here, so I’m posting the question in this comment.
If the admin thinks appropriate, pls help move this comment to a separate post. Thanks for the help!
There is a seemingly fundamental question in causal inference.
Pls forgive my ignorance. Any answer / suggestion / reference / link would be helpful!
==============================
Question:
To decide whether X causes Y, one has to use the do-calculus to compute the average causal effect P(Y|do(X=1))-P(Y|do(X=0)). To use the do-calculus, one has to know the causal graph. But this becomes a chicken-or-egg question: If we know the causal graph, we already know X causes Y or not from the graph. So how to decide whether X causes Y?
Comment by Haoqi — June 26, 2018 @ 5:58 pm
Haoqi –
You got the point, it was exactly the question this blog has started with. The only answer I can propose (for a simple situation like “Does X causally affect Y or not?”, without more complicated causal graph) is either to use kind of empirical analysis at the end of the article https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2984045 or try something from this book https://mitpress.mit.edu/books/elements-causal-inference, where authors, in the beginning, apply two regression (X to Y and Y to X) to detect the directionality of the relationship. I may add, that I’m going to publish the results of the new experiments soon, which will contain some more practical recommendations about separating causal from non-causal relations.
Comment by Igor Mandel — October 25, 2018 @ 6:34 pm