From Melanie Wall, University of Minnesota:
I am teaching a course in latent variable modeling (to biostatistics and other public health students) and was yesterday introducing path analysis concepts including direct and indirect effects.
I showed them how to calculate indirect effects by taking the product of direct paths. Then a student asked about how to interpret the indirect effect and I gave the answer that I always give, that the indirect effect ab (in the following simple model) is the effect that a change in x has on Z through its relationship with Y.
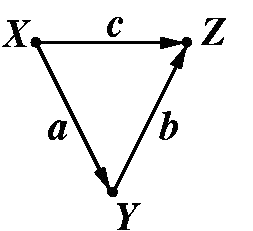
After chewing on this for a second, the student asked the following:
Student: "The interpretation of the b path is: b is the increase we would see in Z given a unit increase in Y while holding X fixed, right?"
Me: "That's right"
Student: "Then what is being held constant when we interpret an indirect effect?"
Me: "Not sure what you mean"
Student: "You said the interpretation of the indirect effect ab is: ab is the increase we would see in Z given a one unit increase in X through its causal effect on Y. But since b (the direct effect from Y to Z) requires X to be held constant how can it be used in a calculation that is also requiring X to change one unit"
Me: "Hmm. Very good question, I'm not sure I have a good answer for you. In the case where the direct path from X Z is zero I think we have no problem since the relationship between Y and Z then has nothing to do with X. But you are right, here if "c" is non-zero then we must interpret b as the effect of Y on Z when X is held constant. I understand that this sounds like it conflicts with the interpretation of the ab indirect effect where we are examining what a change in X will cause. How about I get back to you. As I have told you before, the calculations here aren't hard, its trying to truly understand what your model means that's hard."
Z is zero I think we have no problem since the relationship between Y and Z then has nothing to do with X. But you are right, here if "c" is non-zero then we must interpret b as the effect of Y on Z when X is held constant. I understand that this sounds like it conflicts with the interpretation of the ab indirect effect where we are examining what a change in X will cause. How about I get back to you. As I have told you before, the calculations here aren't hard, its trying to truly understand what your model means that's hard."
From Sampsa Hautaniemi, NIH:
I am at the halfway of your book Causality, which I think to be excellent and instructive. What I am writing to you is that I browsed to homepage of Dr. Lotfi Zadeh and found out that he has a Word document whose subject is 'CAUSALITY IS UNDEFINABLE'. The page is http://www.cs.berkeley.edu/~nikraves/zadeh/Zadeh2.doc. I know you have answered many times reports like that, so if there is already discussion going on of this subject I would appreciate the URL/name of the journal as I am really interested in the subject.
From Erich Battistin, University College, London:
I'm a Ph.D. student in statistics at the Dept. of Economics of UCL, London; in the last few months I went through your papers (and your book) about causality – in particular, I paid more attention to your result on the improvement of Manski's bounds on treatment effects when we have imperfect compliance. This result is certainly powerful but – leaving out technicalities – I don't really understand which information your approach exploits that the one by Manski does not. What is the intuition behind? I didn't find this point explained in any paper I read (but obviously to deal with an 'econometric-based' audience as the one here at UCL you need to make this point clear).
From Les Hayduk, University of Alberta:
Les Hayduk asked whether the operational formula for path coefficient;
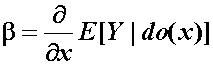 (Eq. 5.24)(Causality, page 161, Eq. (5.24)) is a calculation formula or purely an interpretation formula.
(Eq. 5.24)(Causality, page 161, Eq. (5.24)) is a calculation formula or purely an interpretation formula.
From Professor Nozer Singpurwalla, from The George Washington University:
My basic point is that since causality has not been defined, the causal calculus is a technology which could use a foundation. However, the calculus does give useful insights and is thus valuable. Finally, according to my understanding of the causal calculus, I am inclined to state that the calculus of probability is the calculus of causality, notwithstanding Dennis' [Lindley] concerns about Suppes probabilistic causality.
From Bill Shipley, Universite de Sherbrooke, (Quebec) CANADA:
In most experiments, the external manipulation consists of adding (or subtracting) some amount from X without removing pre-existing causes of X. For example, adding 5 kg/h of fertilizer to a field, adding 5 mg/l of insulin to subjects etc. Here, the pre-existing causes of the manipulated variable still exert effects but a new variable (M) is added.
… The problem that I see with the do(x) operator as a general operator of external manipulation is that it requires two things: (1) removing any pre-existing causes of x and (2) setting x to some value. This corresponds to some types of external manipulations, but not all (or even most) external manipulations. I would introduce an add(x=n) operator, meaning "add, external to the pre-existing causal process, an amount 'n' of x''. Graphically, this consists of augmenting the pre-existing causal graph with a new edge, namely M-n–>X. Algebraically, this would consist of adding a new term –n– as a cause of X.
From L. H., University of Alberta and S.M., Georgia Tech
In response to my comments (e.g., Causality, Section 5.4) that the causal interpretation of structural coefficients is practically unknown among SEM researchers, and my more recent comment that a correct causal interpretation is conspicuously absent from all SEM books and papers, including all 1970-1999 texts in economics, two readers wrote that the "unit-change" interpretation is common and well accepted in the SEM literature.
L.H. from the University of Alberta wrote:
"Page 245 of L. Hayduk, Structural Equation Modeling with LISREL: Essentials and Advances, 1986, has a chapter headed "Interpreting it All", whose first section is titled "The basics of interpretation," whose first paragraph, has a second sentence which says in italics (with notation changed to correspond to the above) that a slope can be interpreted as: the magnitude of the change in y that would be predicted to accompany a unit change in x with the other variables in the equation left untouched at their original values." … "Seems to me that O.D. Duncan, Introduction to Structural Equation Models 1975 pages 1 and 2 are pretty clear on b as causal. "More precisely, it [byx] says that a change of one unit in x … produces a change of b units in y" (page 2). I suspect that H. M. Blalock's book "Causal models in the social Sciences", and D. Heise's book "Causal analysis." probably speak of b as causal."
S.M., from Georgia Tech concurs:
"I concur with L.H. that Heise, author of Causal Analysis (1975) regarded the b of causal equations to be how much a unit change in a cause produced an effect in an effect variable. This is a well-accepted idea."
L.B.S., from University of Arizona, questioned whether the do(x) operator can represent realistic actions or experiments: "Even an otherwise perfectly executed randomized experiment may yield perfectly misleading conclusions if, for example, the construct validity of the treatment is zero, e.g., there is a serious confounding. A good example is a study involving injected vitamin E as a treatment for incubated children at risk for retrolental fibroplasia. The randomized experiment indicated efficacy for the injections, but it was soon discovered that the actual effective treatment was opening the pressurized, oxygen-saturated incubators several times per day to give the injections, thus lowering the barometric pressure and oxygen levels in the blood of the infants (Leonard, Major Medical Mistakes). Any statistical analysis would have been misleading in that case."
S.M., from Georgia Institute of Technology, adds:
"Your example of the misleading causal effect, shows the kind of thing that troubles me about the do(x) concept. You do(x) or don't do(x) but something else, and this seems correlated with an effect. But it may be something else that is correlated with do(x) that is the cause and not the do(x) per se."
From Dennis Lindley
Equations (1.42) and (1.43) and the general issue of description by equations, still perplex me. It is incoherent to state both p(x|y) and p(y|x). (Try it with x and y binary, when these statements describe 4 values, whereas we know only 3 are needed for the joint distribution of x and y.) There are special cases, as with normal, linear regression, where the coherence is avoided. Generally I do not see how there can be two links between x and y.
Apart from the innate symmetricity of structural equation systems, the very definition for the conditional probability as well as Bayes's law of inverse probability unambiguously suggest the reversibility of cause-effect relationships. …
“A is a cause of B only when B can cause A.'' Amen.
(Quoted from Mr. Asha review of Causality, amazon.com, August 29, 2000)
![]() Z is zero I think we have no problem since the relationship between Y and Z then has nothing to do with X. But you are right, here if "c" is non-zero then we must interpret b as the effect of Y on Z when X is held constant. I understand that this sounds like it conflicts with the interpretation of the ab indirect effect where we are examining what a change in X will cause. How about I get back to you. As I have told you before, the calculations here aren't hard, its trying to truly understand what your model means that's hard."
Z is zero I think we have no problem since the relationship between Y and Z then has nothing to do with X. But you are right, here if "c" is non-zero then we must interpret b as the effect of Y on Z when X is held constant. I understand that this sounds like it conflicts with the interpretation of the ab indirect effect where we are examining what a change in X will cause. How about I get back to you. As I have told you before, the calculations here aren't hard, its trying to truly understand what your model means that's hard." 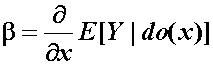 (Eq. 5.24)(Causality, page 161, Eq. (5.24)) is a calculation formula or purely an interpretation formula.
(Eq. 5.24)(Causality, page 161, Eq. (5.24)) is a calculation formula or purely an interpretation formula.