Contributor: Judea Pearl
If you search Google for “Simpson’s paradox,” as I did yesterday, you will get 111,000 results, more than any other statistical paradox that I could name. What elevates this innocent reversal of association to “paradoxical” status, and why it has captured the fascination of statisticians, mathematicians and philosophers for over a century are questions that we discussed at length on this (and other) blogs. The reason I am back to this topic is the publication of four recent papers that give us a panoramic view at how the understanding of causal reasoning has progressed in communities that do not usually participate in our discussions.
As readers of this blog recall, I have been trying since the publication of Causality (2000) to convince statisticians, philosophers and other scientific communities that Simpson’s paradox is: (1) a product of wrongly applied causal principles, and (2) that it can be fully resolved using modern tools of causal inference.
The four papers to be discussed do not fully agree with the proposed resolution.
To reiterate my position, Simpson’s paradox is (quoting Lord Russell) “another relic of a bygone age,” an age when we believed that every peculiarity in the data can be understood and resolved by statistical means. Ironically, Simpson’s paradox has actually become an educational tool for demonstrating the limits of statistical methods, and why causal, rather than statistical considerations are necessary to avoid paradoxical interpretations of data. For example, our recent book Causal Inference in Statistics: A Primer, uses Simpson’s paradox at the very beginning (Section 1.1), to show students the inevitability of causal thinking and the futility of trying to interpret data using statistical tools alone. See http://bayes.cs.ucla.edu/PRIMER/.
Thus, my interest in the four recent articles stems primarily from curiosity to gauge the penetration of causal ideas into communities that were not intimately involved in the development of graphical or counterfactual models. Discussions of Simpson’s paradox provide a sensitive litmus test to measure the acceptance of modern causal thinking. “Talk to me about Simpson,” I often say to friendly colleagues, “and I will tell you how far you are on the causal trail.” (Unfriendly colleagues balk at the idea that there is a trail they might have missed.)
The four papers for discussion are the following:
1.
Malinas, G. and Bigelow, J. “Simpson’s Paradox,” The Stanford Encyclopedia of Philosophy (Summer 2016 Edition), Edward N. Zalta (ed.), URL = <http://plato.stanford.edu/archives/sum2016/entries/paradox-simpson/>.
2.
Spanos, A., “Revisiting Simpson’s Paradox: a statistical misspecification perspective,” ResearchGate Article, <https://www.researchgate.net/publication/302569325>, online May 2016.
<http://arxiv.org/pdf/1605.02209v2.pdf>.
3.
Memetea, S. “Simpson’s Paradox in Epistemology and Decision Theory,” The University of British Columbia (Vancouver), Department of Philosophy, Ph.D. Thesis, May 2015.
https://open.library.ubc.ca/cIRcle/collections/ubctheses/24/items/1.0167719
4.
Bandyopadhyay, P.S., Raghavan, R.V., Deruz, D.W., and Brittan, Jr., G. “Truths about Simpson’s Paradox Saving the Paradox from Falsity,” in Mohua Banerjee and Shankara Narayanan Krishna (Eds.), Logic and Its Applications, Proceedings of the 6th Indian Conference ICLA 2015 , LNCS 8923, Berlin Heidelberg: Springer-Verlag, pp. 58-73, 2015 .
https://www.academia.edu/11600189/Truths_about_Simpson_s_Paradox_Saving_the_Paradox_from_Falsity
——————- Discussion ——————-
1. Molina and Bigelow 2016 (MB)
I will start the discussion with Molina and Bigelow 2016 (MB) because the Stanford Encyclopedia of Philosophy enjoys both high visibility and an aura of authority. MB’s new entry is a welcome revision of their previous article (2004) on “Simpson’s Paradox,” which was written almost entirely from the perspective of “probabilistic causality,” echoing Reichenbach, Suppes, Cartwright, Good, Hesslow, Eells, to cite a few.
Whereas the previous version characterizes Simpson’s reversal as “A Logically Benign, empirically Treacherous Hydra,” the new version dwarfs the dangers of that Hydra and correctly states that Simpson’s paradox poses problem only for “philosophical programs that aim to eliminate or reduce causation to regularities and relations between probabilities.” Now, since the “probabilistic causality” program is fairly much abandoned in the past two decades, we can safely conclude that Simpson’s reversal poses no problem to us mortals. This is reassuring.
MB also acknowledge the role that graphical tools play in deciding whether one should base a decision on the aggregate population or on the partitioned subpopulations, and in testing one’s hypothesized model.
My only disagreement with the MB’s article is that it does not go all the way towards divorcing the discussion from the molds, notation and examples of the “probabilistic causation” era and, naturally, proclaim the paradox “resolved.” By shunning modern notation like do(x), Yx, or their equivalent, the article gives the impression that Bayesian conditionalization, as in P(y|x), is still adequate for discussing Simpson’s paradox, its ramifications and its resolution. It is not.
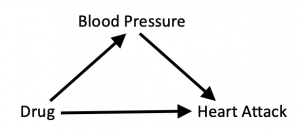
In particular, this notational orthodoxy makes the discussion of the Sure Thing Principle (STP) incomprehensible and obscures the reason why Simpson’s reversal does not constitute a counter example to STP. Specifically, it does not tell readers that causal independence is a necessary condition for the validity of the STP, (i.e., actions should not change the size of the subpopulations) and this independence is violated in the counterexample that Blyth contrived in 1972. (See http://ftp.cs.ucla.edu/pub/stat_ser/r466-reprint.pdf.)
I will end with a humble recommendation to the editors of the Stanford Encyclopedia of Philosophy. Articles concerning causation should be written in a language that permits authors to distinguish causal from statistical dependence. I am sure future authors in this series would enjoy the freedom of saying “treatment does not change gender,” something they cannot say today, using Bayesian conditionalization. However, they will not do so on their own, unless you tell them (and their reviewers) explicitly that it is ok nowadays to deviate from the language of Reichenbach and Suppes and formally state: P(gender|do(treatment)) = P(gender).
Editorial guidance can play an incalculable role in the progress of science.
2. Comments on Spanos (2016)
In 1988, the British econometrician John Denis Sargan gave the following definition of an “economic model”: “A model is the specification of the probability distribution for a set of observations. A structure is the specification of the parameters of that distribution.” (Lectures on Advanced Econometric Theory (1988, p.27))
This definition, still cited in advanced econometric books (e.g., Cameron and Trivdi (2009) Microeconometrics) has served as a credo to a school of economics that has never elevated itself from the data-first paradigm of statistical thinking. Other prominent leaders of this school include Sir David Hendry, who wrote: “The joint density is the basis: SEMs (Structural Equation Models) are merely an interpretation of that.” Members of this school are unable to internalize the hard fact that statistics, however refined, cannot provide the information that economic models must encode to be of use to policy making. For them, a model is just a compact encoding of the density function underlying the data, so, two models encoding the same density function are deemed interchangeable.
Spanos article is a vivid example of how this statistics-minded culture copes with causal problems. Naturally, Spanos attributes the peculiarities of Simpson’s reversal to what he calls “statistical misspecification,” not to causal shortsightedness. “Causal” relationships do not exist in the models of Sargan’s school, so, if anything goes wrong, it must be “statistical misspecification,” what else? But what is this “statistical misspecification” that Spanos hopes would allow him to distinguish valid from invalid inference? I have read the paper several times, and for the life of me, it is beyond my ability to explain how the conditions that Spanos posits as necessary for “statistical adequacy” have anything to do with Simpson’s paradox. Specifically, I cannot see how “misspecified” data, which wrongly claims: “good for men, good for women, bad for people” suddenly becomes “well-specified” when we replace “gender” with “blood pressure”.
Spanos’ conditions for “statistical adequacy” are formulated in the context of the Linear Regression Model and invoke strictly statistical notions such as normality, linearity, independence etc. None of them applies to the binary case of {treatment, gender, outcome} in which Simpson’s paradox is usually cast. I therefore fail to see why replacing “gender” with “blood pressure” would turn an association from “spurious” to “trustworthy”.
Perhaps one of our readers can illuminate the rest of us how to interpret this new proposal. I am at a total loss.
For fairness, I should add that most economists that I know have second thoughts about Sargan’s definition, and claim to understand the distinction between structural and statistical models. This distinction, unfortunately, is still badly missing from econometric textbooks, see http://ftp.cs.ucla.edu/pub/stat_ser/r395.pdf I am sure it will get there some day; Lady Science is forgiving, but what about economics students?
3. Memetea (2015)
Among the four papers under consideration, the one by Memetea, is by far the most advanced, comprehensive and forward thinking. As a thesis written in a philosophy department, Memetea treatise is unique in that it makes a serious and successful effort to break away from the cocoon of “probabilistic causality” and examines Simpson’s paradox to the light of modern causal inference, including graphical models, do-calculus, and counterfactual theories.
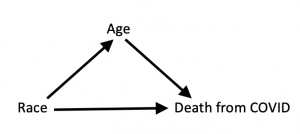
Memetea agrees with our view that the paradox is causal in nature, and that the tools of modern causal analysis are essential for its resolution. She disagrees however with my provocative claim that the paradox is “fully resolved”. The areas where she finds the resolution wanting are mediation cases in which the direct effect (DE) differs in sign from the total effect (TE). The classical example of such cases (Hesslow 1976) tells of a birth control pill that is suspected of producing thrombosis in women and, at the same time, has a negative indirect effect on thrombosis by reducing the rate of pregnancies (pregnancy is known to encourage thrombosis).
I have always argued that Hesslow’s example has nothing to do with Simpson’s paradox because it compares apples and oranges, namely, it compare direct vs. total effects where reversals are commonplace. In other words, Simpson’s reversal evokes no surprise in such cases. For example, I wrote, “we are not at all surprised when smallpox inoculation carries risks of fatal reaction, yet reduces overall mortality by irradicating smallpox. The direct effect (fatal reaction) in this case is negative for every subpopulation, yet the total effect (on mortality) is positive for the population as a whole.” (Quoted from http://ftp.cs.ucla.edu/pub/stat_ser/r436.pdf) When a conflict arises between the direct and total effects, the investigator need only decide what research question represents the practical aspects of the case in question and, once this is done, the appropriate graphical tools should be invoked to properly assess DE or TE. [Recall, complete algorithms are available for both, going beyond simple adjustment, and extending to other counterfactually defined effects (e.g., ETT, causes-of-effect, and more).]
Memetea is not satisfied with this answer. Her condition for resolving Simpson’s paradox requires that the analyst be told whether it is the direct or the total effect that should be the target of investigation. This would require, of course, that the model includes information about the investigator’s ultimate aims, whether alternative interventions are available (e.g. to prevent pregnancy), whether the study result will be used by a policy maker or a curious scientist, whether legal restrictions (e.g., on sex discrimination) apply to the direct or the total effect, and so on. In short, the entire spectrum of scientific and social knowledge should enter into the causal model before we can determine, in any given scenario, whether it is the direct or indirect effect that warrants our attention.
This is a rather tall order to satisfy given that our investigators are fairly good in determining what their research problem is. It should perhaps serve as a realizable goal for artificial intelligence researchers among us, who aim to build an automated scientist some day, capable of reasoning like our best investigators. I do not believe though that we need to wait for that day to declare Simpson’s paradox “resolved”. Alternatively, we can declare it resolved modulo the ability of investigators to define their research problems.
4. Comments on Bandyopadhyay, etal (2015)
There are several motivations behind the resistance to characterize Simpson’s paradox as a causal phenomenon. Some resist because causal relationships are not part of their scientific vocabulary, and some because they think they have discovered a more cogent explanation, which is perhaps easier to demonstrate or communicate.
Spanos’s article represents the first group, while Bandyopadhyay etal’s represents the second. They simulated Simpson’s reversal using urns and balls and argued that, since there are no interventions involved in this setting, merely judgment of conditional probabilities, the fact that people tend to make wrong judgments in this setting proves that Simpson’s surprise is rooted in arithmetic illusion, not in causal misinterpretation.
I have countered this argument in http://ftp.cs.ucla.edu/pub/stat_ser/r414.pdf and I think it is appropriate to repeat the argument here.
“In explaining the surprise, we must first distinguish between ‘Simpson’s reversal’ and ‘Simpson’s paradox’; the former being an arithmetic phenomenon in the calculus of proportions, the latter a psychological phenomenon that evokes surprise and disbelief. A full understanding of Simpson’s paradox should explain why an innocent arithmetic reversal of an association, albeit uncommon, came to be regarded as `paradoxical,’ and why it has captured the fascination of statisticians, mathematicians and philosophers for over a century (though it was first labeled ‘paradox’ by Blyth (1972)) .
“The arithmetics of proportions has its share of peculiarities, no doubt, but these tend to become objects of curiosity once they have been demonstrated and explained away by examples. For instance, naive students of probability may expect the average of a product to equal the product of the averages but quickly learn to guard against such expectations, given a few counterexamples. Likewise, students expect an association measured in a mixture distribution to equal a weighted average of the individual associations. They are surprised, therefore, when ratios of sums, (a+b)/(c+d), are found to be ordered differently than individual ratios, a/c and b/d.1 Again, such arithmetic peculiarities are quickly accommodated by seasoned students as reminders against simplistic reasoning.
“In contrast, an arithmetic peculiarity becomes ‘paradoxical’ when it clashes with deeply held convictions that the peculiarity is impossible, and this occurs when one takes seriously the causal implications of Simpson’s reversal in decision-making contexts. Reversals are indeed impossible whenever the third variable, say age or gender, stands for a pre-treatment covariate because, so the reasoning goes, no drug can be harmful to both males and females yet beneficial to the population as a whole. The universality of this intuition reflects a deeply held and valid conviction that such a drug is physically impossible. Remarkably, such impossibility can be derived mathematically in the calculus of causation in the form of a ‘sure-thing’ theorem (Pearl, 2009, p. 181):
‘An action A that increases the probability of an event B in each subpopulation (of C) must also increase the probability of B in the population as a whole, provided that the action does not change the distribution of the subpopulations.’2
“Thus, regardless of whether effect size is measured by the odds ratio or other comparisons, regardless of whether Z is a confounder or not, and regardless of whether we have the correct causal structure on hand, our intuition should be offended by any effect reversal that appears to accompany the aggregation of data.
“I am not aware of another condition that rules out effect reversal with comparable assertiveness and generality, requiring only that Z not be affected by our action, a requirement satisfied by all treatment-independent covariates Z. Thus, it is hard, if not impossible, to explain the surprise part of Simpson’s reversal without postulating that human intuition is governed by causal calculus together with a persistent tendency to attribute causal interpretation to statistical associations.”
1. In Simpson’s paradox we witness the simultaneous orderings: (a1+b1)/(c1+d1)> (a2+b2)/(c2+d2), (a1/c1)< (a2/c2), and (b1/d1)< (b2/d2)
2. The no-change provision is probabilistic; it permits the action to change the classification of individual units so long as the relative sizes of the subpopulations remain unaltered.
Final Remarks
I used to be extremely impatient with the slow pace in which causal ideas have been penetrating scientific communities that are not used to talk cause-and-effect. Recently, however, I re-read Thomas Kuhn’ classic The Structure of Schientific Revolution and I found there a quote that made me calm, content, even humorous and hopeful. Here it is:
—————- Kuhn —————-
“The transfer of allegiance from paradigm to paradigm is a conversion experience that cannot be forced. Lifelong resistance, particularly from those whose productive careers have committed them to an older tradition of normal science, is not a violation of scientific standards but an index to the nature of scientific research itself.”
p. 151
“Conversions will occur a few at a time until, after the last holdouts have died, the whole profession will again be practicing under a single, but now a different, paradigm.”
p. 152
We are now seeing the last holdouts.
Cheers,
Judea
Addendum: Simpson and the Potential-Outcome Camp
My discussion of the four Simpson’s papers would be incomplete without mentioning another paper, which represents the thinking within the potential outcome camp. The paper in question is “A Fruitful Resolution to Simpson’s Paradox via Multiresolution Inference,” by Keli Liu and Xiao-Li Meng (2014), http://www.stat.columbia.edu/~gelman/stuff_for_blog/LiuMengTASv2.pdf which appeared in the same issue of Statistical Science as my “Understanding Simpson’s Paradox” http://ftp.cs.ucla.edu/pub/stat_ser/r414-reprint.pdf.
The intriguing feature of Liu and Meng’s paper is that they, too, do not see any connection to causality. In their words: “Peeling away the [Simpson’s] paradox is as easy (or hard) as avoiding a comparison of apples and oranges, a concept requiring no mention of causality” p.17, and again: ” The central issues of Simpson’s paradox can be addressed adequately without necessarily invoking causality.” (p. 18). Two comments:
- Liu and Meng fail to see that the distinction between apples and oranges must be made with causal considerations in mind — statistical criteria alone cannot help us avoid a comparison of apples and oranges. This has been shown again and again, even by Simpson himself.
- Liu and Meng do not endorse the resolution offered by causal modeling and, as a result, they end up with the wrong conclusion. Quoting: “Simpson’s Warning: less conditioning is most likely to lead to serious bias when Simpson’s Paradox appears.” (p. 17). Again, Simpson himself brings an example where conditioning leads to more bias, not less.
Thus, in contrast to the data-only economists (Spanos), the potential-outcome camp does not object to causal reasoning per-se, this is their specialty. What they object to are attempts to resolve Simpson’s paradox formally and completely, namely, explicate formally what the differences are between “apples and oranges” and deal squarely with the decision problem: “What to do in case of reversal.”
Why are they resisting the complete solution? Because (and this is a speculation) the complete solution requires graphical tools and we all know the attitude of potential-outcome enthusiasts towards graphs. We dealt with this cultural peculiarity before so, at this point, we should just add Simpson’s paradox to their list of challenges, and resign humbly to the slow pace with which Kuhn’s paradigms are shifting.
Judea