Causal Analysis in Theory and Practice

1. Introduction

This note concerns three papers by Cox and Wermuth (2008; 2014; 2015 (hereforth WC‘08, WC‘14 and CW‘15)) in which they call attention to a class of problems they named “indirect confounding,” where “a much stronger distortion may be introduced than by an unmeasured confounder alone or by a selection bias alone.” We will show that problems classified as “indirect confounding” can be resolved in just a few steps of derivation in do-calculus.

This in itself would not have led me to post a note on this blog, for we have witnessed many difficult problems resolved by formal causal analysis. However, in their three papers, Cox and Wermuth also raise questions regarding the capability and/or adequacy of the do-operator and do-calculus to accurately predict effects of interventions. Thus, a second purpose of this note is to reassure students and users of do-calculus that they can continue to apply these tools with confidence, comfort, and scientifically grounded guarantees.

Finally, I would like to invite the skeptic among my colleagues to re-examine their hesitations and accept causal calculus for what it is: A formal representation of interventions in real world situations, and a worthwhile tool to acquire, use and teach. Among those skeptics I must include colleagues from the potential-outcome camp, whose graph-evading theology is becoming increasing anachronistic (see discussions on this blog, for example, here).

2 Indirect Confounding – An Example

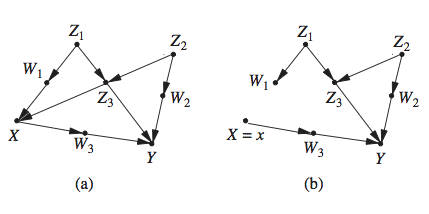
To illustrate indirect confounding, Fig. 1 below depicts the example used in WC‘08, which involves two treatments, one randomized (X), and the other (Z) taken in response to an observation (W) which depends on X. The task is to estimate the direct effect of X on the primary outcome (Y), discarding the effect transmitted through Z.

As we know from elementary theory of mediation (e.g., Causality, p. 127) we cannot block the effect transmitted through Z by simply conditioning on Z, for that would open the spurious path X → W ← U → Y , since W is a collider whose descendant (Z) is instantiated. Instead, we need to hold Z constant by external means, through the do-operator do(Z = z). Accordingly, the problem of estimating the direct effect of X on Y amounts to finding P(y|do(x, z)) since Z is the only other parent of Y (see Pearl (2009, p. 127, Def. 4.5.1)).

Figure 1: An example of “indirect confounding” from WC‘08. Z stands for a treatment taken in response to a test W, whose outcome depend ends on a previous treatment X. U is unobserved. [WC‘08 attribute this example to Robins and Wasserman (1997); an identical structure is treated in Causality, p. 119, Fig. 4.4, as well as in Pearl and Robins (1995).]

Solution:
     P(y|do(x,z))
    =P(y|x, do(z))                             (since X is randomized)
    = ∑_w P(Y|x,w,do(z))P(w|x, do(z))         (by Rule 1 of do-calculus)
    = ∑_w P(Y|x,w,z)P(w|x)               (by Rule 2 and Rule 3 of do-calculus)

We are done, because the last expression consists of estimable factors. What makes this problem appear difficult in the linear model treated by WC‘08 is that the direct effect of X on Y (say α) cannot be identified using a simple adjustment. As we can see from the graph, there is no set S that separates X from Y in Gα. This means that α cannot be estimated as a coefficient in a regression of Y on X and S. Readers of Causality, Chapter 5, would not panic by such revelation, knowing that there are dozens of ways to identify a parameter, going way beyond adjustment (surveyed in Chen and Pearl (2014)). WC‘08 identify α using one of these methods, and their solution coincides of course with the general derivation given above.

The example above demonstrates that the direct effect of X on Y (as well as Z on Y ) can be identified nonparametrically, which extends the linear analysis of WC‘08. It also demonstrates that the effect is identifiable even if we add a direct effect from X to Z, and even if there is an unobserved confounder between X and W – the derivation is almost the same (see Pearl (2009, p. 122)).

Most importantly, readers of Causality also know that, once we write the problem as “Find P(y|do(x, z))” it is essentially solved, because the completeness of the do-calculus together with the algorithmic results of Tian and Shpitser can deliver the answer in polynomial time, and, if terminated with failure, we are assured that the effect is not estimable by any method whatsoever.

3 Conclusions

It is hard to explain why tools of causal inference encounter slower acceptance than tools in any other scientific endeavor. Some say that the difference comes from the fact that humans are born with strong causal intuitions and, so, any formal tool is perceived as a threatening intrusion into one’s private thoughts. Still, the reluctance shown by Cox and Wermuth seems to be of a different kind. Here are a few examples:

Cox and Wermuth (CW’15) write:
“…some of our colleagues have derived a ‘causal calculus’ for the challenging
process of inferring causality; see Pearl (2015). In our view, it is unlikely that
a virtual intervention on a probability distribution, as specified in this calculus,
is an accurate representation of a proper intervention in a given real world
situation.” (p. 3)

These comments are puzzling because the do-operator and its associated “causal calculus” operate not “on a probability distribution,” but on a data generating model (i.e., the DAG). Likewise, the calculus is used, not for “inferring causality” (God forbid!!) but for predicting the effects of interventions from causal assumptions that are already encoded in the DAG.

In WC‘14 we find an even more puzzling description of “virtual intervention”:
“These recorded changes in virtual interventions, even though they are often
called ‘causal effects,’ may tell next to nothing about actual effects in real interventions
with, for instance, completely randomized allocation of patients to
treatments. In such studies, independence result by design and they lead to
missing arrows in well-fitting graphs; see for example Figure 9 below, in the last
subsection.” [our Fig. 1]

“Familiarity is the mother of acceptance,” say the sages (or should have said). I therefore invite my colleagues David Cox and Nanny Wermuth to familiarize themselves with the miracles of do-calculus. Take any causal problem for which you know the answer in advance, submit it for analysis through the do-calculus and marvel with us at the power of the calculus to deliver the correct result in just 3–4 lines of derivation. Alternatively, if we cannot agree on the correct answer, let us simulate it on a computer, using a well specified data-generating model, then marvel at the way do-calculus, given only the graph, is able to predict the effects of (simulated) interventions. I am confident that after such experience all hesitations will turn into endorsements.

BTW, I have offered this exercise repeatedly to colleagues from the potential outcome camp, and the response was uniform: “we do not work on toy problems, we work on real-life problems.” Perhaps this note would entice them to join us, mortals, and try a small problem once, just for sport.

Let’s hope,

Judea

References

Chen, B. and Pearl, J. (2014). Graphical tools for linear structural equation modeling. Tech. Rep. R-432, , Department of Com- puter Science, University of California, Los Angeles, CA. Forthcoming, Psychometrika.
Cox, D. and Wermuth, N. (2015). Design and interpretation of studies: Relevant concepts from the past and some extensions. Observational Studies This issue.
Pearl, J. (2009). Causality: Models, Reasoning, and Inference. 2nd ed. Cambridge Uni- versity Press, New York.
Pearl, J. (2015). Trygve Haavelmo and the emergence of causal calculus. Econometric Theory 31 152–179. Special issue on Haavelmo Centennial.
Pearl, J. and Robins, J. (1995). Probabilistic evaluation of sequential plans from causal models with hidden variables. In Uncertainty in Artificial Intelligence 11 (P. Besnard and S. Hanks, eds.). Morgan Kaufmann, San Francisco, 444–453.
Robins, J. M. and Wasserman, L. (1997). Estimation of effects of sequential treatments by reparameterizing directed acyclic graphs. In Proceedings of the Thirteenth Conference on Uncertainty in Artificial Intelligence (UAI ‘97). Morgan Kaufmann Publishers Inc., San Francisco, CA, USA, 409–420.
Wermuth, N. and Cox, D. (2008). Distortion of effects caused by indirect confounding. Biometrika 95 17–33.
Wermuth, N. and Cox, D. (2014). Graphical Markov models: Overview. ArXiv: 1407.7783.

Our discussion of “causation without manipulation” (link) acquires an added sense of relevance when considered in the context of public concerns with obesity and its consequences. A Reuters story published on September 21 2012 (link) cites a report projecting that at least 44 percent of U.S adults could be obese by 2030, compared to 35.7 percent today, bringing an extra $66 billion a year in obesity-related medical costs. A week earlier, New York City adopted a regulation banning the sale of sugary drinks in containers larger than 16 ounces at restaurants and other outlets regulated by the city health department.

Interestingly, an article published in the International Journal of Obesity {(2008), vol 32, doi:10.1038/i} questions the logic of attributing consequences to obesity. The authors, M A Hernan and S L Taubman (both of Harvard’s School of Public Health) imply that the very notion of “obesity-related medical costs” is undefined, if not misleading and that, instead of speaking of “obesity shortening life” or “obesity raising medical costs”, one should be speaking of manipulable variables like “life style” or “soda consumption” as causing whatever harm we tend to attribute to obesity.

The technical rational for these claims is summarized in their abstract:
“We argue that observational studies of obesity and mortality violate the condition of consistency of counterfactual (potential) outcomes, a necessary condition for meaningful causal inference, because (1) they do not explicitly specify the interventions on body mass index (BMI) that are being compared and (2) different methods to modify BMI may lead to different counterfactual mortality outcomes, even if they lead to the same BMI value in a given person.

Readers will surely notice that these arguments stand in contradiction to the structural, as well as closest-world definitions of counterfactuals (Causality, pp. 202-206, 238-240), according to which consistency is a theorem in counterfactual logic, not an assumption and, therefore, counterfactuals are always consistent (link). A counterfactual appears to be inconsistent when its antecedant A (as in “had A been true”) is conflated with an external intervention devised to enforce the truth of A. Practical interventions tend to have side effects, and these need to be reckoned with in estimation, but counterfactuals and causal effects are defined independently of those interventions and should not, therefore, be denied existence by the latter’s imperfections. To say that obesity has no intrinsic effects because some interventions have side effects is analogous to saying that stars do not move because telescopes have imperfections.

Rephrased in a language familiar to readers of this blog Hernan and Taubman claim that the causal effect P(mortality=y|Set(obesity=x)) is undefined, seemingly because the consequences of obesity depend on how we choose to manipulate it. Since the probability of death will generally depend on whether you manipulate obesity through diet versus, say, exercise. (We assume that we are able to perfectly define quantitative measures of obesity and mortality), Hernan and Taubman conclude that P(mortality=y|Set(obesity=x)) is not formally a function of x, but a one-to-many mapping.

This contradicts, of course, what the quantity P(Y=y|Set(X=x)) represents. As one who coined the symbols Set(X=x) (Pearl, 1993) [it was later changed to do(X=x)] I can testify that, in its original conception:

1. P(mortality = y| Set(obesity = x) does not depend on any choice of intervention; it is defined relative to a hypothetical, minimal intervention needed for establishing X=x and, so, it is defined independently of how the event obesity=x actually came about.

2. While it is true that the probability of death will generally depend on whether we manipulate obesity through diet versus, say, exercise, the quantity P(mortality=y|Set(obesity=x)) has nothing to do with diet or exercise, it has to do only with the level x of X and the anatomical or social processes that respond to this level of X. Set(obesity=x) describes a virtual intervention, by which nature sets obesity to x, independent of diet or exercise, while keeping everything else in tact, especially the processes that respond to X. The fact that we, mortals, cannot execute such incisive intervention, does not make this intervention (1) undefined, or (2) vague, or (3) replaceable by manipulation-dependent operators.

To elaborate:
(1) The causal effects of obesity are well-defined in the SEM model, which consists of functions, not manipulations.

(2) The causal effects of obesity are as clear and transparent as the concept of functional dependency and were chosen in fact to serve as standards of scientific communication (See again Wikipedia, Cholesterol, how relationships are defined by “absence” or “presence” of agents not by the means through which those agents are controlled.

(3) If we wish to define a new operator, say Set_a(X=x), where $a$ stands for the means used in achieving X=x (as Larry Wasserman suggested), this can be done within the syntax of the do-calculus, But that would be a new operator altogether, unrelated to do(X=x) which is manipulation-neutral.

There are several ways of loading the Set(X=x) operator with manipulational or observational specificity. In the obesity context, one may wish to consider P(mortality=y|Set(diet=z)) or P(mortality=y|Set(exercise=w)) or P(mortality=y|Set(exercise=w), Set(diet=z)) or P(mortality=y|Set(exercise=w), See (diet=z)) or P(mortality=y|See(obesity=x), Set(diet=z)) The latter corresponds to the studies criticized by Hernan and Taubman, where one manipulates diet and passively observes Obesity. All these variants are legitimate quantities that one may wish to evaluate, if called for, but have nothing to do with P(mortality=y|Set(obesity =x)) which is manipulation-neutral..

Under certain conditions we can even infer P(mortality=y|Set(obesity =x)) from data obtained under dietary controlled experiments. [i.e., data governed by P(mortality=y|See(obesity=x), Set(diet=z)); See R-397.) But these conditions can only reveal themselves to researchers who acknowledge the existence of P(mortality=y|Set(obesity=x)) and are willing to explore its properties.

Additionally, all these variants can be defined and evaluated in SEM and, moreover, the modeler need not think about them in the construction of the model, where only one relation matters: Y LISTENS TO X.

My position on the issues of manipulation and SEM can be summarized as follows:

1. The fact that morbidity varies with the way we choose to manipulate obesity (e.g., diet, exercise) does not diminish our need, or ability to define a manipulation-neutral notion of “the effect of obesity on morbidity”, which is often a legitimate target of scientific investigation, and may serve to inform manipulation-specific effects of obesity.

2. In addition to defining and providing identification conditions for the manipulation-neutral notion of “effect of obesity on morbidity”, the SEM framework also provides formal definitions and identification conditions for each of the many manipulation-specific effects of obesity, and this can be accomplished through a single SEM model provided that the version-specific characteristics of those manipulations are encoded in the model.

I would like to say more about the relationship between knowledge-based statements (e.g., “obesity kills”) and policy-specific statements (e.g., “Soda kills.”) I wrote a short note about it in the Journal of Causal Inference http://ftp.cs.ucla.edu/pub/stat_ser/r422.pdf and I think it would add another perspective to our discussion. A copy of the introduction section is given below.

Is Scientific Knowledge Useful for Policy Analysis?
A Peculiar Theorem Says: No
(from http://ftp.cs.ucla.edu/pub/stat_ser/r422.pdf)

1 Introduction
In her book, Hunting Causes and Using Them [1], Nancy Cartwright expresses several objections to the do(x) operator and the “surgery” semantics on which it is based (pp. 72 and 201). One of her objections concerned the fact that the do-operator represents an ideal, atomic intervention, different from the one implementable by most policies under evaluation. According to Cartwright, for policy evaluation we generally want to know what would happen were the policy really set in place, and the policy may affect a host of changes in other variables in the system, some envisaged and some not.

In my answer to Cartwright [2, p. 363], I stressed two points. First, the do-calculus enables us to evaluate the effect of compound interventions as well, as long as they are described in the model and are not left to guesswork. Second, I claimed that in many studies our goal is not to predict the effect of the crude, non-atomic intervention that we are about to implement but, rather, to evaluate an ideal, atomic policy that cannot be implemented given the available tools, but that represents nevertheless scientific knowledge that is pivotal for our understanding of the domain.

The example I used was as follows: Smoking cannot be stopped by any legal or educational means available to us today; cigarette advertising can. That does not stop researchers from aiming to estimate “the effect of smoking on cancer,” and doing so from experiments in which they vary the instrument — cigarette advertisement — not smoking. The reason they would be interested in the atomic intervention P(Cancer|do(Smoking)) rather than (or in addition to) P(cancer|do(advertising)) is that the former represents a stable biological characteristic of the population, uncontaminated by social factors that affect susceptibility to advertisement, thus rendering it transportable across cultures and environments. With the help of this stable characteristic, one can assess the effects of a wide variety of practical policies, each employing a different smoking-reduction instrument. For example, if careful scientific investigations reveal that smoking has no effect on cancer, we can comfortably conclude that increasing cigarette taxes will not decrease cancer rates and that it is futile for schools to invest resources in anti-smoking educational programs. This note takes another look at this argument, in light of recent results in transportability theory (Bareinboim and Pearl [3], hereafter BP).

Robert Platt called my attention to the fact that there is a fundamental difference between Smoking and Obesity; randomization is physically feasible in the case of smoking (say, in North Korea) — not in the case of obesity.

I agree; it would have been more effective to use Obesity instead of Smoking in my response to Cartwright. An RCT experiment on Smoking can be envisioned, (if one is willing to discount obvious side effect of forced smoking or forced withdrawal) while RCT on Obesity requires more creative imagination; not through a powerful dictator, but through an agent such as Lady Nature herself, who can increase obesity by one unit and evaluate its consequences on various body functions.

This is what the do-operator does, it simulates an experiment conducted by Lady Nature who, for all that we know is all mighty, and can permit all the organisms that are affected by BMI (and fat content etc etc [I assume here that we can come to some consensus on the vector of measurements that characterizes Obesity]) to respond to a unit increase of BMI in the same way that they responded in the past. Moreover, she is able to do it by an extremely delicate surgery, without touching those variables that we mortals need to change in order to drive BMI up or down.

This is not a new agent by any means, it is the standard agent of science. For example, consider the 1st law of thermodynamic, PV =n R T. While Volume (V), Temperature (T) and the amount of gas (n) are independently manipulable, pressure (P) is not. This means that whenever we talk about the pressure changing, it is always accompanied by a change in V, n and/or T which, like diet and exercise, have their own side effects. Does this prevent us from speaking about the causal effect of tire pressure on how bumpy the road is? Must we always mention V, T or n when we speak about the effect of air pressure on the size of the balloon we are blowing? Of course not.! Pressure has life of its own (the rate of momentum transfer to a wall that separates two vessels ) independent on the means by which we change it.

Aha!!! The skeptic argues: “Things are nice in physics, but epidemiology is much more complex, we do not know the equations or the laws, and we will never in our lifetime know the detailed anatomy of the human body. This ignorance-pleading argument always manages to win the hearts of the mystic, especially among researchers who feel uncomfortable encoding partial scientific knowledge in a model. Yet Lady Nature does not wait for us to know things before she makes our heart muscle respond to the fat content in the blood. And we need not know the exact response to postulate that such response exists.

Scientific thinking is not unique to physics. Consider any standard medical test and let’s ask ourselves whether the quantities measured have “well-defined causal effects” on the human body. Does “blood pressure” have any effect on anything? Why do we not hear complaints about “blood pressure” being “not well defined”.? After all, following the criterion of Hernan and Taubman (2008), the “effect of X on Y” is ill-defined whenever Y depends on the means we use to change X. So “blood pressure” has no well defined
effect on any organ in the human body. The same goes for “blood count” “kidney function” …. Rheumatoid Factor…. If these variables have no effects on anything why do we measure them? Why do physicians communicate with each other through these measurements, instead of through the “interventions” that may change these measurements?

My last comment is for epidemiologists who see their mission as that of “changing the world for the better” and, in that sense, they only *care* about treatments (causal variables) that are manipulable. I have only admiration for this mission. However, to figure out which of those treatments should be applied in any given situation, we need to understand the situation and, it so happened that “understanding” involves causal relationships between manipulable as well as non-manipulable variables. For instance, if someone offers to sell you a new miracle drug that (provenly) reduces obesity, and your scientific understanding is that obesity has no effect whatsoever on anything that is important to you, then, regardless of other means that are available for manipulating obesity you would tell the salesman to go fly a kite. And you would do so regardless of whether those other means produced positive or negative results. The basis for rejecting the new drug is precisely your understanding that “Obesity has no effect on outcome”, the very quantity that some of epidemiologists now wish to purge from science, all in the name of only caring about manipulable treatments.

Epidemiology, as well as all empirical sciences need both scientific and clinical knowledge to sustain and communicate that which we have learned and to advance beyond it. While the effects of diet and exercise are important for controlling obesity, the health consequences of obesity are no less important; they constitute legitimate targets of scientific pursuit, regardless of current shortcomings in clinical knowledge.

Judea

The second part of our latest post “David Freedman, Statistics, and Structural Equation Models” (May 6, 2015) has stimulated a lively email discussion among colleagues from several disciplines. In what follows, I will be sharing the highlights of the discussion, together with my own position on the issue of manipulability.

Many of the discussants noted that manipulability is strongly associated (if not equated) with “comfort of interpretation”. For example, we feel more comfortable interpreting sentences of the type “If we do A, then B would be more likely” compared with sentences of the type “If A were true, then B would be more likely”. Some attribute this association to the fact that empirical researchers (say epidemiologists) are interested exclusively in interventions and preventions, not in hypothetical speculations about possible states of the world. The question was raised as to why we get this sense of comfort. Reference was made to the new book by Tyler VanderWeele, where this question is answered quite eloquently:

“It is easier to imagine the rest of the universe being just as it is if a patient took pill A rather than pill B than it is trying to imagine what else in the universe would have had to be different if the temperature yesterday had been 30 degrees rather than 40. It may be the case that human actions, seem sufficiently free that we have an easier time imagining only one specific action being different, and nothing else.”
(T. Vanderweele, “Explanation in causal Inference” p. 453-455)

This sensation of discomfort with non-manipulable causation stands in contrast to the practice of SEM analysis, in which causes are represented as relations among interacting variables, free of external manipulation. To explain this contrast, I note that we should not overlook the purpose for which SEM was created — the representation of scientific knowledge. Even if we agree with the notion that the ultimate purpose of all knowledge is to guide actions and policies, not to engage in hypothetical speculations, the question still remains: How do we encode this knowledge in the mind (or in textbooks) so that it can be accessed, communicated, updated and used to guide actions and policies. By “how” I am concerned with the code, the notation, its
syntax and its format.

There was a time when empirical scientists could dismiss questions of this sort (i.e., “how do we encode”) as psychological curiosa, residing outside the province of “objective” science. But now that we have entered the enterprise of causal inference, and we express concerns over the comfort and discomfort of interpreting counterfactual utterances, we no longer have the luxury of ignoring those questions; we must ask: how do scientists encode knowledge, because this question holds the key to the distinction between the comfortable and the uncomfortable, the clear versus the ambiguous.

The reason I prefer the SEM specification of knowledge over a manipulation-restricted specification comes from the realization that SEM matches the format in which humans store scientific knowledge. (Recall, by “SEM” we mean a manipulation-free society of variables, each listening to the others and each responding to what it hears) In support of this realization, I would like to copy below a paragraph from Wikipedia’s entry on Cholesterol, section on “Clinical Significance.” (It is about 20 lines long but worth a serious linguistic analysis).

——————–from Wikipedia, dated 5/10/15 —————
According to the lipid hypothesis , abnormal cholesterol levels ( hyperchol esterolemia ) or, more properly, higher concentrations of LDL particles and lower concentrations of functional HDL particles are strongly associated with cardiovascular disease because these promote atheroma development in arteries ( atherosclerosis ). This disease process leads to myocardial infraction (heart attack), stroke, and peripheral vascular disease . Since higher blood LDL, especially higher LDL particle concentrations and smaller LDL particle size, contribute to this process more than the cholesterol content of the HDL particles, LDL particles are often termed “bad cholesterol” because they have been linked to atheroma formation. On the other hand, high concentrations of functional HDL, which can remove cholesterol from cells and atheroma, offer protection and are sometimes referred to as “good cholesterol”. These balances are mostly genetically determined, but can be changed by body build, medications , food choices, and other factors. [ 54 ] Resistin , a protein secreted by fat tissue, has been shown to increase the production of LDL in human liver cells and also degrades LDL receptors in the liver. As a result, the liver is less able to clear cholesterol from the bloodstream. Resistin accelerates the accumulation of LDL in arteries, increasing the risk of heart disease. Resistin also adversely impacts the effects of statins, the main cholesterol-reducing drug used in the treatment and prevention of cardiovascular disease.
————-end of quote ——————

My point in quoting this paragraph is to show that, even in “clinical significance” sections, most of the relationships are predicated upon states of variables, as opposed to manipulations of variables. They talk about being “present” or “absent”, being at high concentration or low concentration, smaller particles or larger particles; they talk about variables “enabling,” “disabling,” “promoting,” “leading to,” “contributing to,” etc. Only two of the sentences refer directly to exogenous manipulations, as in “can be changed by body build, medications, food choices…”

This manipulation-free society of sensors and responders that we call “scientific knowledge” is not oblivious to the world of actions and interventions; it was actually created to (1) guide future actions and (2) learn from interventions.

(1) The first frontier is well known. Given a fully specified SEM, we can predict the effect of compound interventions, both static and time varying, pre-planned or dynamic. Moreover, given a partially specified SEM (e.g., a DAG) we can often use data to fill in the missing parts and predict the effect of such interventions. These require however that the interventions be specified by “setting” the values of one or several variables. When the action of interest is more complex, say a disjunctive action like: “paint the wall green or blue” or “practice at least 15 minutes a day”, a more elaborate machinery is needed to infer its effects from the atomic actions and counterfactuals that the model encodes (See http://ftp.cs.ucla.edu/pub/stat_ser/r359.pdf and Hernan etal 2011.) Such derivations are nevertheless feasible from SEM without enumerating the effects of all disjunctive actions of the form “do A or B” (which is obviously infeasible).

(2) The second frontier, learning from interventions, is less developed. We can of course check, using the methods above, whether a given SEM is compatible with the results of experimental studies (Causality, Def.1.3.1). We can also determine the structure of an SEM from a systematic sequence of experimental studies. What we are still lacking though are methods of incremental updating, i.e., given an SEM M and an experimental study that is incompatible with M, modify M so as to match the new study, without violating previous studies, though only their ramifications are encoded in M.

Going back to the sensation of discomfort that people usually express vis a vis non-manipulable causes, should such discomfort bother users of SEM when confronting non-manipulable causes in their model? More concretely, should the difficulty of imagining “what else in the universe would have had to be different if the temperature yesterday had been 30 degrees rather than 40,” be a reason for misinterpreting a model that contains variables labeled “temperature” (the cause) and “sweating” (the effect)? My answer is: No. At the deductive phase of the analysis, when we have a fully specified model before us, the model tells us precisely what else would be different if the temperature yesterday had been 30 degrees rather than 40.”

Consider the sentence “Mary would not have gotten pregnant had she been a man”. I believe most of us would agree with the truth of this sentence despite the fact that we may not have a clue what else in the universe would have had to be different had Mary been a man. And if the model is any good, it would imply that regardless of other things being different (e.g. Mary’s education, income, self esteem etc.) she would not have gotten pregnant. Therefore, the phrase “had she been a man” should not be automatically rejected by interventionists as meaningless — it is quite meaningful.

Now consider the sentence: “If Mary were a man, her salary would be higher.” Here the discomfort is usually higher, presumably because not only we cannot imagine what else in the universe would have had to be different had Mary been a man, but those things (education, self esteem etc.) now make a difference in the outcome (salary). Are we justified now in declaring discomfort? Not when we are reading our model. Given a fully specified SEM, in which gender, education, income, and self esteem are bonified variables, one can compute precisely how those factors should be affected by a gender change. Complaints about “how do we know” are legitimate at the model construction phase, but not when we assume having a fully specified model before us, and merely ask for its ramifications.

To summarize, I believe the discomfort with non-manipulated causes represents a confusion between model utilization and model construction. In the former phase counterfactual sentences are well defined regardless of whether the antecedent is manipulable. It is only when we are asked to evaluate a counterfactual sentence by intuitive, unaided judgment, that we feel discomfort and we are provoked to question whether the counterfactual is “well defined”. Counterfactuals are always well defined relative to a given model, regardless of whether the antecedent is manipulable or not.

This takes us to the key question of whether our models should be informed by the the manipulability restriction and how. Interventionists attempt to convince us that the very concept of causation hinges on manipulability and, hence, that a causal model void of manipulability information is incomplete, if not meaningless. We saw above that SEM, as a representation of scientific knowledge, manages quite well without the manipulability restriction. I would therefore be eager to hear from interventionists what their conception is of “scientific knowledge”, and whether they can envision an alternative to SEM which is informed by the manipulability restriction, and yet provides a parsimonious account of that which we know about the world.

My appeal to interventionists to provide alternatives to SEM has so far not been successful. Perhaps readers care to suggest some? The comment section below is open for suggestions, disputations and clarifications.

(Re-edited: 5/6/15, 4 pm)

Michael A Lewis (Hunter College) sent us the following query:

Dear Judea,
I was reading a book by the late statistician David Freedman and in it he uses the term “response schedule” to refer to an equation which represents a causal relationship between variables. It appears that he’s using that term as a synonym for “structural equation” the one you use. In your view, am I correct in regarding these as synonyms? Also, Freedman seemed to be of the belief that response schedules only make sense if the causal variable can be regarded as amenable to manipulation. So variables like race, gender, maybe even socioeconomic status, etc. cannot sensibly be regarded as causes since they can’t be manipulated. I’m wondering what your view is of this manipulation perspective.
Michael

—
My answer is: Yes. Freedman’s “response schedule” is a synonym for “structural equation.” The reason why Freedman did not say so explicitly has to do with his long and rather bumpy journey from statistical to causal thinking. Freedman, like most statisticians in the 1980’s could not make sense of the Structural Equation Models (SEM) that social scientists (e.g., Duncan) and econometricians (e.g., Goldberger) have adopted for representing causal relations. As a result, he criticized and ridiculed this enterprise relentlessly. In his (1987) paper “As others see us,” for example, he went as far as “proving” that the entire enterprise is grounded in logical contradictions. The fact that SEM researchers at that time could not defend their enterprise effectively (they were as confused about SEM as statisticians — judging by the way they responded to his paper) only intensified Freedman criticism. It continued well into the 1990’s, with renewed attacks on anything connected with causality, including the causal search program of Spirtes, Glymour and Scheines.

I have had a long and friendly correspondence with Freedman since 1993 and, going over a file of over 200 emails, it appears that it was around 1994 when he began to convert to causal thinking. First through the do-operator (by his own admission) and, later, by realizing that structural equations offer a neat way of encoding counterfactuals.

I speculate that the reason Freedman could not say plainly that causality is based on structural equations was that it would have been too hard for him to admit that he was in error criticizing a model that he misunderstood, and, that is so simple to understand. This oversight was not entirely his fault; for someone trying to understand the world from a statistical view point, structural equations do not make any sense; the asymmetric nature of the equations and those slippery “error terms” stand outside the prism of the statistical paradigm. Indeed, even today, very few statisticians feel comfortable in the company of structural equations. (How many statistics textbooks do we know that discuss structural equations?)

So, what do you do when you come to realize that a concept you ridiculed for 20 years is the key to understanding causation? Freedman decided not to say “I erred”, but to argue that the concept was not rigorous enough for statisticians to understood. He thus formalized “response schedule” and treated it as a novel mathematical object. The fact is, however, that if we strip “response schedule” from its superlatives, we find that it is just what you and I call a “function”. i.e., a mapping between the states of one variable onto the states of another. Some of Freedman’s disciples are admiring this invention (See R. Berk’s 2004 book on regression) but most people that I know just look at it and say: This is what a structural equation is.

The story of David Freedman is the story of statistical science itself and the painful journey the field has taken through the causal reformation. Starting with the structural equations of Sewal Wright (1921), and going through Freedman’s “response schedule”, the field still can’t swallow the fundamental building block of scientific thinking, in which Nature is encoded as a society of sensing and responding variables. Funny, econometrics is yet to start its reformation, though it has been housing SEM since Haavelmo (1943). (How many econometrics textbooks do we know which teach students how to read counterfactuals from structural equations?).

—
I now go to your second question, concerning the mantra “no causation without manipulation.” I do not believe anyone takes this slogan as a restriction nowadays, including its authors, Holland and Rubin. It will remain a relic of an era when statisticians tried to define causation with the only mental tool available to them: the randomized controlled trial (RCT).

I summed it up in Causality, 2009, p. 361: “To suppress talk about how gender causes the many biological, social, and psychological distinctions between males an females is to suppress 90% of our knowledge about gender differences”

I further elaborated on this issue in (Bollen and Pearl 2014 p. 313) saying:

“Pearl (2011) further shows that this restriction has led to harmful consequence by forcing investigators to compromise their research questions only to avoid the manipulability restriction. The essential ingredient of causation, as argued in Pearl (2009: 361), is responsiveness, namely, the capacity of some variables to respond to variations in other variables, regardless of how those variations came about.”

In (Causality 2009 p. 361) I also find this paragraph: “It is for that reason, perhaps, that scientists invented counterfactuals; it permit them to state and conceive the realization of antecedent conditions without specifying the physical means by which these conditions are established;”

All in all, you have touched on one of the most fascinating chapters in the history of science, featuring a respectable scientific community that clings desperately to an outdated dogma, while resisting, adamantly, the light that shines around it. This chapter deserves a major headline in Kuhn’s book on scientific revolutions. As I once wrote: “It is easier to teach Copernicus in the Vatican than discuss causation with a statistician.” But this was in the 1990’s, before causal inference became fashionable. Today, after a vicious 100-year war of reformation, things are begining to change (See http://www.nasonline.org/programs/sackler-colloquia/completed_colloquia/Big-data.html). I hope your upcoming book further accelerates the transition.

Flower 1 — Seeing counterfactuals in graphs

Some critics of structural equations models and their associated graphs have complained that those graphs depict only observable variables but: “You can’t see the counterfactuals in the graph.” I will soon show that this is not the case; counterfactuals can in fact be seen in the graph, and I regard it as one of many flowers blooming out of the First Law of Causal Inference (see here). But, first, let us ask why anyone would be interested in locating counterfactuals in the graph.

This is not a rhetorical question. Those who deny the usefulness of graphs will surely not yearn to find counterfactuals there. For example, researchers in the Imbens-Rubin camp who, ostensibly, encode all scientific knowledge in the “Science” = Pr(W,X,Y(0),Y(1)), can, theoretically, answer all questions about counterfactuals straight from the “science”; they do not need graphs.

On the other extreme we have students of SEM, for whom counterfactuals are but byproducts of the structural model (as the First Law dictates); so, they too do not need to see counterfactuals explicitly in their graphs. For these researchers, policy intervention questions do not require counterfactuals, because those can be answered directly from the SEM-graph, in which the nodes are observed variables. The same applies to most counterfactual questions, for example, the effect of treatment on the treated (ETT) and mediation problems; graphical criteria have been developed to determine their identification conditions, as well as their resulting estimands (see here and here).

So, who needs to see counterfactual variables explicitly in the graph?

There are two camps of researchers who may benefit from such representation. First, researchers in the Morgan-Winship camp (link here) who are using, interchangeably, both graphs and potential outcomes. These researchers prefer to do the analysis using probability calculus, treating counterfactuals as ordinary random variables, and use graphs only when the algebra becomes helpless. Helplessness arises, for example, when one needs to verify whether causal assumptions that are required in the algebraic derivations (e.g., ignorability conditions) hold true in one’s model of reality. These researchers understand that “one’s model of reality” means one’s graph, not the “Science” = Pr(W,X,Y(0),Y(1)), which is cognitively inaccessible. So, although most of the needed assumptions can be verified without counterfactuals from the SEM-graphs itself (e.g., through the back door condition), the fact that their algebraic expressions already carry counterfactual variables makes it more convenient to see those variables represented explicitly in the graph.

The second camp of researchers are those who do not believe that scientific knowledge is necessarily encoded in an SEM-graph. For them, the “Science” = Pr(W,X,Y(0),Y(1)), is the source of all knowledge and assumptions, and a graph may be constructed, if needed, as an auxiliary tool to represent sets of conditional independencies that hold in Pr(*). [I was surprised to discover sizable camps of such researchers in political science and biostatistics; possibly because they were exposed to potential outcomes prior to studying structural equation models.] These researchers may resort to other graphical representations of independencies, not necessarily SEM-graphs, but occasionally seek the comfort of the meaningful SEM-graph to facilitate counterfactual manipulations. Naturally, they would prefer to see counterfactual variables represented as nodes on the SEM-graph, and use d-separation to verify conditional independencies, when needed.

After this long introduction, let us see where the counterfactuals are in an SEM-graph. They can be located in two ways, first, augmenting the graph with new nodes that represent the counterfactuals and, second, mutilate the graph slightly and use existing nodes to represent the counterfactuals.

The first method is illustrated in chapter 11 of Causality (2nd Ed.) and can be accessed directly here. The idea is simple: According to the structural definition of counterfactuals, Y(0) (similarly Y(1)) represents the value of Y under a condition where X is held constant at X=0. Statistical variations of Y(0) would therefore be governed by all exogenous variables capable of influencing Y when X is held constant, i.e. when the arrows entering X are removed. We are done, because connecting these variables to a new node labeled Y(0), Y(1) creates the desired representation of the counterfactual. The book-section linked above illustrates this construction in visual details.

The second method mutilates the graph and uses the outcome node, Y, as a temporary surrogate for Y(x), with the understanding that the substitution is valid only under the mutilation. The mutilation required for this substitution is dictated by the First Law, and calls for removing all arrows entering the treatment variable X, as illustrated in the following graph (taken from here).

This method has some disadvantages compared with the first; the removal of X’s parents prevents us from seeing connections that might exist between Y_x and the pre-intervention treatment node X (as well as its descendants). To remedy this weakness, Shpitser and Pearl (2009) (link here) retained a copy of the pre-intervention X node, and kept it distinct from the manipulated X node.

Equivalently, Richardson and Robins (2013) spliced the X node into two parts, one to represent the pre-intervention variable X and the other to represent the constant X=x.

All in all, regardless of which variant you choose, the counterfactuals of interest can be represented as nodes in the structural graph, and inter-connections among these nodes can be used either to verify identification conditions or to facilitate algebraic operations in counterfactual logic.

Note, however, that all these variants stem from the First Law, Y(x) = Y[M_x], which DEFINES counterfactuals in terms of an operation on a structural equation model M.

Finally, to celebrate this “Flower of the First Law” and, thereby, the unification of the structural and potential outcome frameworks, I am posting a flowery photo of Don Rubin and myself, taken during Don’s recent visit to UCLA.

In several papers and lectures I have used the rhetorical title “The First Law of Causal Inference” when referring to the structural definition of counterfactuals:

The more I talk with colleagues and students, the more I am convinced that the equation deserves the title. In this post, I will explain why.

As many readers of Causality (Ch. 7) would recognize, Eq. (1) defines the potential-outcome, or counterfactual, Y_x(u) in terms of a structural equation model M and a submodel, M_x, in which the equations determining X is replaced by a constant X=x. Computationally, the definition is straightforward. It says that, if you want to compute the counterfactual Y_x(u), namely, to predict the value that Y would take, had X been x (in unit U=u), all you need to do is, first, mutilate the model, replace the equation for X with X=x and, second, solve for Y. What you get IS the counterfactual Y_x(u). Nothing could be simpler.

So, why is it so “fundamental”? Because from this definition we can also get probabilities on counterfactuals (once we assign probabilities, P(U=u), to the units), joint probabilities of counterfactuals and observables, conditional independencies over counterfactuals, graphical visualization of potential outcomes, and many more. [Including, of course, Rubin’s “science”, Pr(X,Y(0),(Y1))]. In short, we get everything that an astute causal analyst would ever wish to define or estimate, given that he/she is into solving serious problems in causal analysis, say policy analysis, or attribution, or mediation. Eq. (1) is “fundamental” because everything that can be said about counterfactuals can also be derived from this definition.
[See the following papers for illustration and operationalization of this definition:
http://ftp.cs.ucla.edu/pub/stat_ser/r431.pdf
http://ftp.cs.ucla.edu/pub/stat_ser/r391.pdf
http://ftp.cs.ucla.edu/pub/stat_ser/r370.pdf
also, Causality chapter 7.]

However, it recently occurred on me that the conceptual significance of this definition is not fully understood among causal analysts, not only among “potential outcome” enthusiasts, but also among structural equations researchers who practice causal analysis in the tradition of Sewall Wright, O.D. Duncan, and Trygve Haavelmo. Commenting on the flood of methods and results that emerge from this simple definition, some writers view it as a mathematical gimmick that, while worthy of attention, need to be guarded with suspicion. Others labeled it “an approach” that need be considered together with “other approaches” to causal reasoning, but not as a definition that justifies and unifies those other approaches.

Even authors who advocate a symbiotic approach to causal inference — graphical and counterfactuals — occasionally fail to realize that the definition above provides the logic for any such symbiosis, and that it constitutes in fact the semantical basis for the potential-outcome framework.

I will start by addressing the non-statisticians among us; i.e., economists, social scientists, psychometricians, epidemiologists, geneticists, metereologists, environmental scientists and more, namely, empirical scientists who have been trained to build models of reality to assist in analyzing data that reality generates. To these readers I want to assure that, in talking about model M, I am not talking about a newly invented mathematical object, but about your favorite and familiar model that has served as your faithful oracle and guiding light since college days, the one that has kept you cozy and comfortable whenever data misbehaved. Yes, I am talking about the equation

that you put down when your professor asked: How would household spending vary with income, or, how would earning increase with education, or how would cholesterol level change with diet, or how would the length of the spring vary with the weight that loads it. In short, I am talking about innocent equations that describe what we assume about the world. They now call them “structural equations” or SEM in order not to confuse them with regression equations, but that does not make them more of a mystery than apple pie or pickled herring. Admittedly, they are a bit mysterious to statisticians, because statistics textbooks rarely acknowledge their existence [Historians of statistics, take notes!] but, otherwise, they are the most common way of expressing our perception of how nature operates: A society of equations, each describing what nature listens to before determining the value it assigns to each variable in the domain.

Why am I elaborating on this perception of nature? To allay any fears that what is put into M is some magical super-smart algorithm that computes counterfactuals to impress the novice, or to spitefully prove that potential outcomes need no SUTVA, nor manipulation, nor missing data imputation; M is none other but your favorite model of nature and, yet, please bear with me, this tiny model is capable of generating, on demand, all conceivable counterfactuals: Y(0),Y(1), Y_x, Y_{127}, X_z, Z(X(y)) etc. on and on. Moreover, every time you compute these potential outcomes using Eq. (1) they will obey the consistency rule, and their probabilities will obey the laws of probability calculus and the graphoid axioms. And, if your model justifies “ignorability” or “conditional ignorability,” these too will be respected in the generated counterfactuals. In other words, ignorability conditions need not be postulated as auxiliary constraints to justify the use of available statistical methods; no, they are derivable from your own understanding of how nature operates.

In short, it is a miracle.

Not really! It should be self evident. Couterfactuals must be built on the familiar if we wish to explain why people communicate with counterfactuals starting at age 4 (“Why is it broken?” “Lets pretend we can fly”). The same applies to science; scientists have communicated with counterfactuals for hundreds of years, even though the notation and mathematical machinery needed for handling counterfactuals were made available to them only in the 20th century. This means that the conceptual basis for a logic of counterfactuals resides already within the scientific view of the world, and need not be crafted from scratch; it need not divorce itself from the scientific view of the world. It surely should not divorce itself from scientific knowledge, which is the source of all valid assumptions, or from the format in which scientific knowledge is stored, namely, SEM.

Here I am referring to people who claim that potential outcomes are not explicitly represented in SEM, and explicitness is important. First, this is not entirely true. I can see (Y(0), Y(1)) in the SEM graph as explicitly as I see whether ignorability holds there or not. [See, for example, Fig. 11.7, page 343 in Causality]. Second, once we accept SEM as the origin of potential outcomes, as defined by Eq. (1), counterfactual expressions can enter our mathematics proudly and explicitly, with all the inferential machinery that the First Law dictates. Third, consider by analogy the teaching of calculus. It is feasible to teach calculus as a stand-alone symbolic discipline without ever mentioning the fact that y'(x) is the slope of the function y=f(x) at point x. It is feasible, but not desirable, because it is helpful to remember that f(x) comes first, and all other symbols of calculus, e.g., f'(x), f”(x), [f(x)/x]’, etc. are derivable from one object, f(x). Likewise, all the rules of differentiation are derived from interpreting y'(x) as the slope of y=f(x).

Where am I heading?
First, I would have liked to convince potential outcome enthusiasts that they are doing harm to their students by banning structural equations from their discourse, thus denying them awareness of the scientific basis of potential outcomes. But this attempted persuasion has been going on for the past two decades and, judging by the recent exchange with Guido Imbens (link), we are not closer to an understanding than we were in 1995. Even an explicit demonstration of how a toy problem would be solved in the two languages (link) did not yield any result.

Second, I would like to call the attention of SEM practitioners, including of course econometricians, quantitative psychologists and political scientists, and explain the significance of Eq. (1) in their fields. To them, I wish to say: If you are familiar with SEM, then you have all the mathematical machinery necessary to join the ranks of modern causal analysis; your SEM equations (hopefully in nonparametric form) are the engine for generating and understanding counterfactuals.; True, your teachers did not alert you to this capability; it is not their fault, they did not know of it either. But you can now take advantage of what the First Law of causal inference tells you. You are sitting on a gold mine, use it.

Finally, I would like to reach out to authors of traditional textbooks who wish to introduce a chapter or two on modern methods of causal analysis. I have seen several books that devote 10 chapters on SEM framework: identification, structural parameters, confounding, instrumental variables, selection models, exogeneity, model misspecification, etc., and then add a chapter to introduce potential outcomes and cause-effect analyses as useful new comers, yet alien to the rest of the book. This leaves students to wonder whether the first 10 chapters were worth the labor. Eq. (1) tells us that modern tools of causal analysis are not new comers, but follow organically from the SEM framework. Consequently, one can leverage the study of SEM to make causal analysis more palatable and meaningful.

Please note that I have not mentioned graphs in this discussion; the reason is simple, graphical modeling constitutes The Second Law of Causal Inference.

Enjoy both,
Judea

A lively discussion flared up early this month on Andrew Gelman’s blog (garnering 114 comments!) which should be of some interest to readers of this blog.

The discussion started by a quote from George Box (1979) on the advantages of model-based approaches, and drifted into related topics such as

(1) What is a model-based approach,

(2) Whether mainstream statistics encourages this approach,

(3) Whether statistics textbooks and education have given face to reality,

(4) Whether a practicing statistician should invest time learning causal modeling,

or wait till it “proves itself” in the real messy world?

I share highlights of this discussion here, because I believe many readers have faced similar disputations and misunderstandings in conversations with pre-causal statisticians.

To read more, click here.

Judea Pearl Writes:

For a long time I could not figure out why SEM researchers find it hard to embrace the “causal inference approach” to mediation, which is based on counterfactuals. My recent conversations with David Kenny and Bengt Muthen have opened my eyes, and I am now pretty sure that I have found both the obstacle and the key to making causal mediation an organic part of SEM research.

Here is the key:

Why are we tempted to “control for” the mediator M when we wish to estimate the direct effect of X on Y? The reason is that, if we succeed in preventing M from changing then whatever changes we measure in Y are attributable solely to variations in X and we are justified then in proclaiming the effect observed as “direct effect of X on Y”. Unfortunately , the language of probability theory does not possess the notation to express the idea of “preventing M from changing” or “physically holding M constant”. The only operation probability allows us to use is “conditioning” which is what we do when we “control for M” in the conventional way (i.e., let M vary, but ignore all samples except those that match a specified value of M). This habit is just plain wrong, and is the mother of many confusions in the practice of SEM.

To find out why, you are invited to visit: http://ftp.cs.ucla.edu/pub/stat_ser/r421.pdf, paragraph starting with “In the remaining of this note, …”, on page 2.

Best,
Judea

A recent article by Heckman and Pinto (HP) (link: http://www.nber.org/papers/w19453.pdf) discusses the do-calculus as a formal operationalization of Haavelmo’s approach to policy intervention. HP replace the do-operator with an equivalent operator, called “fix,” which simulates a Fisherian experiment with randomized “do”. They advocate the use of “fix,” discover limitations in “do,” and inform readers that those limitations disappear in “the Haavelmo approach.”

I examine the logic of HP’s paper, its factual basis, and its impact on econometric research and education (link: http://ftp.cs.ucla.edu/pub/stat_ser/r420.pdf).

From Dr. Patrik Hoyer (University of Helsinki, Finland):

I have a hard time understanding what counterfactuals are actually useful for. To me, they seem to be answering the wrong question. In your book, you give at least a couple of different reasons for when one would need the answer to a counterfactual question, so let me tackle these separately:

1. Legal questions of responsibility. From your text, I infer that the American legal system says that a defendant is guilty if he or she caused the plaintiff's misfortune. You take this to mean that if the plaintiff had not suffered misfortune had the defendant not acted the way he or she did, then the defendant is to be sentenced. So we have a counterfactual question that needs to be determined to establish responsibility. But in my mind, the law is clearly flawed. Responsibility should rest with the predicted outcome of the defendant's action, not with what actually happened. Let me take a simple example: say that I am playing a simple dice-game for my team. Two dice are to be thrown and I am to bet on either (a) two sixes are thrown, or (b) anything else comes up. If I guess correctly, my team wins a dollar, if I guess wrongly, my team loses a dollar. I bet (b), but am unlucky and two sixes actually come up. My team loses a dollar. Am I responsible for my team's failure? Surely, in the counterfactual sense yes: had I bet differently my team would have won. But any reasonable person on the team would thank me for betting the way I did. In the same fashion, a doctor should not be held responsible if he administers, for a serious disease, a drug which cures 99.99999% of the population but kills 0.00001%, even if he was unlucky and his patient died. If the law is based on the counterfactual notion of responsibility then the law is seriously flawed, in my mind.

   A further example is that on page 323 of your book: the desert traveler. Surely, both Enemy-1 and Enemy-2 are equally 'guilty' for trying to murder the traveler. Attempted murder should equal murder. In my mind, the only rationale for giving a shorter sentence for attempted murder is that the defendant is apparently not so good at murdering people so it is not so important to lock him away… (?!)

2. The use of context in decision-making. On page 217, you write "At this point, it is worth emphasizing that the problem of computing counterfactual expectations is not an academic exercise; it represents in fact the typical case in almost every decision-making situation." I agree that context is important in decision making, but do not agree that we need to answer counterfactual questions.

   In decision making, the things we want to estimate is P(future | do(action), see(context) ). This is of course a regular do-probability, not a counterfactual query. So why do we need to compute counterfactuals?

   In your example in section 7.2.1, your query (3): "Given that the current price is P=p₀, what would be the expected value of the demand Q if we were to control the price at P=p₁?". You argue that this is counterfactual. But what if we introduce into the graph new variables Qtomorrow and Ptomorrow, with parent sets (U₁, I, Ptomorrow) and (W,U)2,Qtomorrow), respectively, and with the same connection-strengths d₁, d₂, b₂, and b₁. Now query (3) reads: "Given that we observe P=p₀, what would be the expected value of the demand Qtomorrow if we perform the action do(Ptomorrow=p₁)?" This is the same exact question but it is not counterfactual, it is just P(Qtomorrow | do(Ptomorrow=p₁), see(P=P₀)). Obviously, we get the correct answer by doing the counterfactual analysis, but the question per se is no longer counterfactual and can be computed using regular do( )-machinery. I guess this is the idea of your 'twin network' method of computing counterfactuals. In this case, why say that we are computing a counterfactual when what we really want is prediction (i.e. a regular do-expression)?

3. In the latter part of your book, you use counterfactuals to define concepts such as 'the cause of X' or 'necessary and sufficient cause of Y'. Again, I can understand that it is tempting to mathematically define such concepts since they are in use in everyday language, but I do not think that this is generally very helpful. Why do we need to know 'the cause' of a particular event? Yes, we are interested in knowing 'causes' of events in the sense that they allows us to predict the future, but this is again a case of point (2) above.

   To put it in the most simplified form, my argument is the following: Regardless of if we represent individuals, businesses, organizations, or government, we are constantly faced with decisions of how to act (and these are the only decisions we have!). What we want to know is, what will likely happen if we act in particular ways. So we want to know is P(future | do(action), see(context) ). We do not want nor need the answers to counterfactuals.

Where does my reasoning go wrong?