Flowers of the First Law of Causal Inference
Flower 1 — Seeing counterfactuals in graphs
Some critics of structural equations models and their associated graphs have complained that those graphs depict only observable variables but: “You can’t see the counterfactuals in the graph.” I will soon show that this is not the case; counterfactuals can in fact be seen in the graph, and I regard it as one of many flowers blooming out of the First Law of Causal Inference (see here). But, first, let us ask why anyone would be interested in locating counterfactuals in the graph.
This is not a rhetorical question. Those who deny the usefulness of graphs will surely not yearn to find counterfactuals there. For example, researchers in the Imbens-Rubin camp who, ostensibly, encode all scientific knowledge in the “Science” = Pr(W,X,Y(0),Y(1)), can, theoretically, answer all questions about counterfactuals straight from the “science”; they do not need graphs.
On the other extreme we have students of SEM, for whom counterfactuals are but byproducts of the structural model (as the First Law dictates); so, they too do not need to see counterfactuals explicitly in their graphs. For these researchers, policy intervention questions do not require counterfactuals, because those can be answered directly from the SEM-graph, in which the nodes are observed variables. The same applies to most counterfactual questions, for example, the effect of treatment on the treated (ETT) and mediation problems; graphical criteria have been developed to determine their identification conditions, as well as their resulting estimands (see here and here).
So, who needs to see counterfactual variables explicitly in the graph?
There are two camps of researchers who may benefit from such representation. First, researchers in the Morgan-Winship camp (link here) who are using, interchangeably, both graphs and potential outcomes. These researchers prefer to do the analysis using probability calculus, treating counterfactuals as ordinary random variables, and use graphs only when the algebra becomes helpless. Helplessness arises, for example, when one needs to verify whether causal assumptions that are required in the algebraic derivations (e.g., ignorability conditions) hold true in one’s model of reality. These researchers understand that “one’s model of reality” means one’s graph, not the “Science” = Pr(W,X,Y(0),Y(1)), which is cognitively inaccessible. So, although most of the needed assumptions can be verified without counterfactuals from the SEM-graphs itself (e.g., through the back door condition), the fact that their algebraic expressions already carry counterfactual variables makes it more convenient to see those variables represented explicitly in the graph.
The second camp of researchers are those who do not believe that scientific knowledge is necessarily encoded in an SEM-graph. For them, the “Science” = Pr(W,X,Y(0),Y(1)), is the source of all knowledge and assumptions, and a graph may be constructed, if needed, as an auxiliary tool to represent sets of conditional independencies that hold in Pr(*). [I was surprised to discover sizable camps of such researchers in political science and biostatistics; possibly because they were exposed to potential outcomes prior to studying structural equation models.] These researchers may resort to other graphical representations of independencies, not necessarily SEM-graphs, but occasionally seek the comfort of the meaningful SEM-graph to facilitate counterfactual manipulations. Naturally, they would prefer to see counterfactual variables represented as nodes on the SEM-graph, and use d-separation to verify conditional independencies, when needed.
After this long introduction, let us see where the counterfactuals are in an SEM-graph. They can be located in two ways, first, augmenting the graph with new nodes that represent the counterfactuals and, second, mutilate the graph slightly and use existing nodes to represent the counterfactuals.
The first method is illustrated in chapter 11 of Causality (2nd Ed.) and can be accessed directly here. The idea is simple: According to the structural definition of counterfactuals, Y(0) (similarly Y(1)) represents the value of Y under a condition where X is held constant at X=0. Statistical variations of Y(0) would therefore be governed by all exogenous variables capable of influencing Y when X is held constant, i.e. when the arrows entering X are removed. We are done, because connecting these variables to a new node labeled Y(0), Y(1) creates the desired representation of the counterfactual. The book-section linked above illustrates this construction in visual details.
The second method mutilates the graph and uses the outcome node, Y, as a temporary surrogate for Y(x), with the understanding that the substitution is valid only under the mutilation. The mutilation required for this substitution is dictated by the First Law, and calls for removing all arrows entering the treatment variable X, as illustrated in the following graph (taken from here).
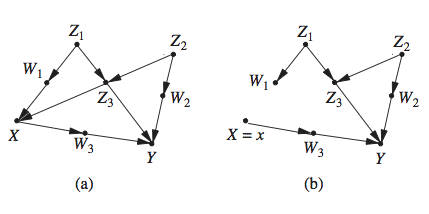
This method has some disadvantages compared with the first; the removal of X’s parents prevents us from seeing connections that might exist between Y_x and the pre-intervention treatment node X (as well as its descendants). To remedy this weakness, Shpitser and Pearl (2009) (link here) retained a copy of the pre-intervention X node, and kept it distinct from the manipulated X node.
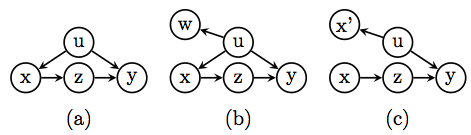
Equivalently, Richardson and Robins (2013) spliced the X node into two parts, one to represent the pre-intervention variable X and the other to represent the constant X=x.
All in all, regardless of which variant you choose, the counterfactuals of interest can be represented as nodes in the structural graph, and inter-connections among these nodes can be used either to verify identification conditions or to facilitate algebraic operations in counterfactual logic.
Note, however, that all these variants stem from the First Law, Y(x) = Y[M_x], which DEFINES counterfactuals in terms of an operation on a structural equation model M.
Finally, to celebrate this “Flower of the First Law” and, thereby, the unification of the structural and potential outcome frameworks, I am posting a flowery photo of Don Rubin and myself, taken during Don’s recent visit to UCLA.

Dear Judea,
Perhaps this is just me, but I feel that adding counterfactual nodes make the graph too cumbersome.
I’m trying to think of a situation where you have 4 levels of X (0,1,2,3). Y(0)=Y(1)=Y(2) (i.e. no arrow from X to Y when X=0,1,2), and Y(0) is not equal to Y(3) (i.e. an arrow from X to Y when X=3). Putting all this in a single graph, to my view, makes it too complicated.
-Conrad.
Comment by Conrad — December 22, 2014 @ 2:23 pm
Dear Conrad,
You are absolutely right. No one would load the graph with ALL counterfactuals; their
number is super exponential. Rather, the needed counterfactual is generated upon demands, for example, when we wish to
test whether a given counterfactual is independent on another give some variable. We then generate
the nodes, test for independence, and remove them, only to wait for another query.
The example you brought up illustrates that, indeed,
the counterfactual node created needs to be a conjunction of all counterfactual variables {Y(x1), Y(x2),….,Y(xn)}
If this joint variable satisfies the independence queried, then any subset satisfies it. Conversely, when we say
that the omitted factor, or “disturbance term” is independent of something, we mean that each of its instantiation is
independent of that something.
It is for this reason that I find it more meaningful to judge independence of “omitted factors” than independence
of conjunctions of counterfactuals like {Y(x1), Y(x2),….,Y(xn)}. Some researchers think the latter is more
scientific, and only by writing down the latter you show that “you know what you are talking about”.
I am for flowers.
Judea
Comment by judea — December 23, 2014 @ 6:34 am
Dear Judea,
Representing counterfactuals in a manner that could make them ‘visible’ for even laymen out there is on my agenda too, of course. This comes from arriving in the statistics field through the SEM backdoor (and a chunk of physics college work), which added some challenges to grasping common statistical entities, but empowered me with a visual understanding mechanism that still benefits me.
One such SEM object that can be stretched so it can cover many common entities is the latent variable of course, which I have thrown upon things that were not commonly considered LVs as such, like propensity scores (existing ‘out there’ but never fully accessible), and now even counterfactuals. I know you wrote about such a representation option too, for me it became obvious when trying to ‘see’ these variables with my own eyes, in a data format, like a worksheet: where are these two Y(x0) and Y(x1) variables (under say two treatment conditions 0 and 1), and what makes them ‘disappear’ when nature (or researchers) opt for one vs. the other one? And where do they go, are they gone forever, or can we resurrect them for some autopsies, when needed?
With 2 such options, as Conrad pointed out, ‘seeing’ them is much easier than with a continuous X range of possibilities, of course. But one can literally see them, I’ve shown this to myself and others from the MMM conference (thanks for coming over there, of course, that put me on this counterfactuals adventure path!) http://scholar.google.com/scholar?cluster=6396546620311161616&hl=en&oi=scholarr
I benefited from the Wang & Sobel 2013 chapter too, where they posed a challenge to SEMers, which I will detail on SEMNET for some resolution soon, they also used the visual display of the ‘variables’: seeing Y(x0) and Y(x1) and Y [observed] as 3 such ‘variables’ makes things much easier to grasp, especially when assigning meaning to statements about ‘ignorability’ or such: for SEMers one can now think of relations between 100% observed (or observable) variables, 50% observable ones by nature (like Y(x0) and Y(x1), in an experiment with a 0 and a 1 condition, both are missing 1/2 of the ‘values’ by design), or 100% unobservable by design, like the Y(M1(0)), or Y when X=0, but for M under X=1.
I was able to ‘see’ then that some claims are made at the “all Y’s” level, where one sees 3 such Ys, or even more, when mediator is considered, like ignorability, whereas others are at the observed/observable variables level only, which is a subset of the ‘many Y’s’ set. And that one simply needs to keep things straight in their mind when talking about causality assumptions and claims, and be aware of skipping from one level to another (and back), like when explaining why ignorability cannot be tested with observed data: we talk about correlations between variables that are missing 1/2 of their values, but complementary such halfs unfortunately.
I am trying to bring such insights (still developing) into the LV representations in SEM, like a Y being literally a composite of such many Y latents (the two in my example above only), although for now I see only an imagery/visual-grasp benefit to it. Anyways, good that you are pointing to the different ‘traditions’ out there, as I am working my way through Morgan and Winship, and Shpitser, and others. I’ll try to provide some translational advice to SEMers on a blog soon, I need a bit more critical mass I guess.
Nice flowers!
Comment by Emil Coman — December 26, 2014 @ 1:26 pm
Dear Emil,
Thank you for giving us an insight into the difficulties faced by SEM researchers trying to reconcile “potential outcome” idioms with traditional SEM framework. But, for the life of me, I still do not understand what drove you into this painful journey. As I said in my post above, SEM researchers do not need to ask whether (Y(1),Y(0)) are independent on other variables, nor to see these counterfactuals explicitly in their model.
Quoting :
“On the other extreme we have students of SEM, for whom counterfactuals are but byproducts of the structural model (as the First Law dictates); so, they too do not need to see counterfactuals explicitly in their graphs. For these researchers, policy intervention questions do not require counterfactuals, because those can be answered directly from the SEM-graph, in which the nodes are observed variables. The same applies to most counterfactual questions, for example, the effect of treatment on the treated (ETT) and mediation problems; graphical criteria have been developed to determine their identification conditions, as well as their resulting estimands (see here and here).
So, who needs to see counterfactual variables explicitly in the graph?
Can you describe to us what research problem drove you into this journey? Here, I mean a genuine research question (e.g., needed to estimate XXX, from data YYY, given assumptions ZZZ) not merely an intellectual curiosity to understand what Wang and Sobel are saying in their article.(on which Bollen and I commented elsewhere, see R-393).
Now, assuming that it was merely an intellectual curiosity to understand the new talk in town, “potential outcomes”, “ignorability” etc etc. Did you find anything missing from my translation: “(Y(0),Y(1)) are none others but what SEMers
call “error terms” or “missing factors”, i.e., the factors that cause Y to vary when X is held constant (at zero or at one).” Nothing more to it.
In posting after posting I have been trying to tell SEMers: counterfactuals grow organically in you own garden, they are simple to understand and simple to analyze with conventional SEM language, much much simpler than what you would find
in the ignorability-speaking literature. (This is why I posted the First Law and its flowers).
From your comment, I gather that I was not very convincing, and that there is perhaps something I left out.
I am eager to find out what it is, so that I can post another flower, for fun and insight.
Judea
Comment by judea pearl — December 27, 2014 @ 6:18 am
[…] “Flowers”. The first tells us how counterfactuals can be seen in the causal graph (link), and the second clarifies questions concerned with conditioning on post-treatment variables. […]
Pingback by Causal Analysis in Theory and Practice » Winter Greeting from the UCLA Causality Blog — January 27, 2015 @ 7:34 am
[…] our examination of “the flowers of the First Law” (see previous flowers here and here) this posting looks at one of the most crucial questions in causal inference: “How […]
Pingback by Causal Analysis in Theory and Practice » Flowers of the First Law of Causal Inference (Flower #3) — April 24, 2015 @ 8:51 pm