Causal inference without graphs
In a recent posting on this blog, Elias and Bryant described how graphical methods can help decide if a pseudo-randomized variable, Z, qualifies as an instrumental variable, namely, if it satisfies the exogeneity and exclusion requirements associated with the definition of an instrument. In this note, I aim to describe how inferences of this type can be performed without graphs, using the language of potential outcome. This description should give students of causality an objective comparison of graph-less vs. graph-based inferences. See my exchange with Guido Imbens [here].
Every problem of causal inference must commence with a set of untestable, theoretical assumptions that the modeler is prepared to defend on scientific grounds. In structural modeling, these assumptions are encoded in a causal graph through missing arrows and missing latent variables. Graphless methods encode these same assumptions symbolically, using two types of statements:
1. Exclusion restrictions, and
2. Conditional independencies among observable and potential outcomes.
For example, consider the causal Markov chain 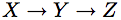 which represents the structural equations:
which represents the structural equations:

with 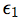 and
and 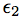 being omitted factors such that X,
being omitted factors such that X, 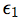 ,
, 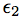 are mutually independent.
are mutually independent.
These same assumptions can also be encoded in the language of counterfactuals, as follows:

(3) represents the missing arrow from X to Z, and (4)-(6) convey the mutual independence of X, 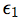 , and
, and 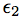 .
.
[Remark: General rules for translating graphical models to counterfactual notation are given in Pearl (2009, pp. 232-234).]
Assume now that we are given the four counterfactual statements (3)-(6) as a specification of a model; What machinery can we use to answer questions that typically come up in causal inference tasks? One such question is, for example, is the model testable? In other words, is there an empirical test conducted on the observed variables X, Y, and Z that could prove (3)-(6) wrong? We note that none of the four defining conditions (3)-(6) is testable in isolation, because each invokes an unmeasured counterfactual entity. On the other hand, the fact the equivalent graphical model advertises the conditional independence of X and Z given Y, X _||_ Z | Y, implies that the combination of all four counterfactual statements should yield this testable implication.
Another question often posed to causal inference is that of identifiability, for example, whether the
causal effect of X on Z is estimable from observational studies.
Whereas graphical models enjoy inferential tools such as d-separation and do-calculus, potential-outcome specifications can use the axioms of counterfactual logic (Galles and Pearl 1998, Halpern, 1998) to determine identification and testable implication. In a recent paper, I have combined the graphoid and counterfactual axioms to provide such symbolic machinery (link).
However, the aim of this note is not to teach potential outcome researchers how to derive the logical consequences of their assumptions but, rather, to give researchers the flavor of what these derivation entail, and the kind of problems the potential outcome specification presents vis a vis the graphical representation.
As most of us would agree, the chain 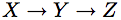 appears more friendly than the 4 equations in (3)-(6), and the reasons are both representational and inferential. On the representational side we note that it would take a person (even an expert in potential outcome) a pause or two to affirm that (3)-(6) indeed represent the chain process he/she has in mind. More specifically, it would take a pause or two to check if some condition is missing from the list, or whether one of the conditions listed is redundant (i.e., follows logically from the other three) or whether the set is consistent (i.e., no statement has its negation follows from the other three). These mental checks are immediate in the graphical representation; the first, because each link in the graph corresponds to a physical process in nature, and the last two because the graph is inherently consistent and non-redundant. As to the inferential part, using the graphoid+counterfactual axioms as inference rule is computationally intractable. These axioms are good for confirming a derivation if one is proposed, but not for finding a derivation when one is needed.
appears more friendly than the 4 equations in (3)-(6), and the reasons are both representational and inferential. On the representational side we note that it would take a person (even an expert in potential outcome) a pause or two to affirm that (3)-(6) indeed represent the chain process he/she has in mind. More specifically, it would take a pause or two to check if some condition is missing from the list, or whether one of the conditions listed is redundant (i.e., follows logically from the other three) or whether the set is consistent (i.e., no statement has its negation follows from the other three). These mental checks are immediate in the graphical representation; the first, because each link in the graph corresponds to a physical process in nature, and the last two because the graph is inherently consistent and non-redundant. As to the inferential part, using the graphoid+counterfactual axioms as inference rule is computationally intractable. These axioms are good for confirming a derivation if one is proposed, but not for finding a derivation when one is needed.
I believe that even a cursory attempt to answer research questions using (3)-(5) would convince the reader of the merits of the graphical representation. However, the reader of this blog is already biased, having been told that (3)-(5) is the potential-outcome equivalent of the chain X—>Y—>Z. A deeper appreciation can be reached by examining a new problem, specified in potential- outcome vocabulary, but without its graphical mirror.
Assume you are given the following statements as a specification.
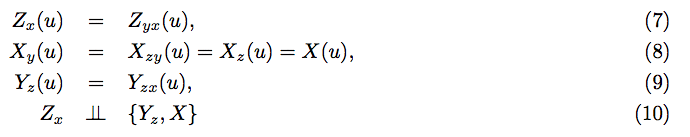
It represents a familiar model in causal analysis that has been throughly analyzed. To appreciate the power of graphs, the reader is invited to examine this representation above and to answer a few questions:
a) Is the process described familiar to you?
b) Which assumption are you willing to defend in your interpretation of the story.
c) Is the causal effect of X on Y identifiable?
d) Is the model testable?
I would be eager to hear from readers
1. if my comparison is fair.
2. which argument they find most convincing.
Dear Judea,
In the comment by Bryant and Elias they mentioned the LATE (Local Average Treatment Effect) concept. I am still curious as to how we can infer/read from the causal graph that this average effect is identified. It is straightforward in the potential outcome framework where it was introduced.
Guido
Comment by guido imbens — November 9, 2014 @ 6:37 pm
We replied in the original post, link: http://www.mii.ucla.edu/causality/?p=1241&cpage=1#comment-305210
Comment by eb — November 9, 2014 @ 8:47 pm
Dear Guido,
You asked again how we can read from a graph that LATE is identified. This is easy. We first ask the graph if the IV conditions are satisfied. If the graph says Yes, we convert the assumptions in the graph to a format that can accept algebraic manipuations, we then invite the rules of inference we learned from the axiomatization of structural counterfactuals, and we apply them, to find out under what conditions identification will be feasible. Exactly the way you derived LATE, except that we are aware of (1) the assumptions and work done in preparing the problem for algebraic manipulations, and (2) the validity of our rules of inference.
I will be more specific.
Graphs are non-parametric abstractions of structural models, designed to deliver all the ramifications of the structure without making any commitment to the form of the equations or to the distribution of the error terms. Obviously, if a mathematical object is instructed to ignore the form of the equations, it cannot, on its own, answer questions about the specifics of one form or another. For that reason, no one should expect the graph alone to tell us if LATE is identified, since LATE invokes restrictions on the functions. When stronger assumptions about the equations are deemed plausible (e.g., monotonicity or compliance) graphs are used in symbiosis with algebraic inference rules to identify additional causal parameters, such as LATE. Their role in this symbiosis is to ratify conditions that are needed for the derivation, (e.g., conditional independencies) and that are not explicit in the algebraic representation.
In your derivation of LATE you must have invoked such rules of inference, for example, the rules of conditional independence, consistency, composition, etc. The soundness and completeness of these rules of inference emanate from the structural semantics of counterfactuals, (Balke and Pearl, 1994, Halpern 1998) and I am not aware of an alternative semantics supporting the validity these rules. So, in this sense, the logical basis for the derivation of LATE is provided by the structural-algebraic symbiosis. Other results obtained through this symbiosis are equally impressive; for example, the instrumental inequality, causal mediation, causes of effects, actual causation, effect of treatment on the treated, targeted estimation, external validity, selection bias, missing data and more. Some of these results and applications are mentioned in Causality, chapters 7-10, others flourish in related literature, especially in epidemiology and SEM.
Somehow, West-and-Koch missed this point. By saying that “there is much to be gained by also considering other [approaches]” they implied that those other approaches were excluded from the graphical-algebraic umbrella advocated in my book — they were not excluded. My book devotes 36 pages to the potential outcome approach (see index) and many more pages to counterfactuals, which are potential-outcomes without the arrow-phobia. My students derive LATE in homework #7 of my causal inference class, my papers are loaded with counterfactual notation and potential outcome derivations, both prospective and retrospective. Exclusion is not in our culture.
At the same time, we cannot join the chanting of “some problems do not need graphs” because we recognize that any problem that seems to need no graphs has undergone a long process of reformating before graphless methods become applicable and, even then, the assumptions needed are still comprehesible only in the language of graphs. Please examine the two examples above, and to tell us whether this assumption is comprehensible: X_||_Y_x | W1, W2 . And lets not go back to claiming that W1 and W2 are not present in LATE. I think Elias and Bryant covered this claim by asking how you propose to rule out possible threats to exclusion and exogeneity assumptions.
I hope we can summarize this exchange by jointly endorsing the merits of the graphical-algebraic symbiosis.
Are you prepared to join me?
Comment by judea pearl — November 11, 2014 @ 1:47 am
Dear Guido, perhaps I can explain why this topic evokes strong emotion for many of us.
Speaking as a scientist, I like graphical models. I like them because they represent networks of relationships. Networks are fundamentally important for representing systems and I think that studying systems is what scientists, in general, want to be able to do. I believe that all problems are ultimately system problems, as no elements live in complete isolation. It certainly seems to me that the potential outcome framework, like most of the models of traditional statistics, is not designed for investigating network hypotheses about systems. To the extent that one only wishes to study reductionist relationships, say the net effect of an exposure on a response, and go no further, then there are non-graphical approaches that can perhaps be sufficient in some cases. Where this gets touchy for me is when authoritative voices, and there are many amongst statisticians, recommend against structural equation modeling because the models are too complex. Those voices, whether they intend to or not, are declaring that we practicing scientists should not quantitatively evaluate complex network hypotheses; i.e., that we should not study systems. The lead paragraph for my webpage states my opinion on this.
“Science and society are moving from a historical emphasis on individual processes to a concern about entire systems. The complexity of the world in which we live, along with the increased level of our ambitions, now cause us to want to understand systems and predict, as much as we can, their behavior. Understanding systems requires approaches that permit both the discovery and extrapolation of system structure. Analytically, systems are often represented as networks of interacting elements, thus the business of studying systems can be approached using methods for studying causal networks.”
Sincerely,
Jim Grace
Comment by Jim Grace — November 11, 2014 @ 11:28 am
Dear Jim,
I have no disagreement with anything you write. Networks are fascinating concepts. Part of this summer I spent working with some researchers at Facebook on causal problems in such settings. To me it seemed that potential outcomes can bring a lot to those problems. See for example the work by Aronow and Samii at Yale. Perhaps causal graphs are also useful there. There are lot of interesting problems there, and the more methods for handling them the better.
For me it also gets touchy when authoritative voices declare what we should and should not be doing. That is why I strongly object to statements like Judea’s claim: “There was a time when people settled differences by saying: Oh, it is just a different approach to the same problem, each person may choose the argument he/she finds most persuasive, let a thousand flowers bloom, there are dozen roads to Rome, etc. That era has ended with the development of objective criteria of tractability and feasibility.” Scholars should make up their own minds and statements likes the quote in my view diminish the tremendous accomplishments of Judea and the causal graph community.
Respectfully,
Guido Imbens
Comment by guido imbens — November 11, 2014 @ 12:12 pm
[…] in 1995. Even an explicit demonstration of how a toy problem would be solved in the two languages (link) did not yield any […]
Pingback by Causal Analysis in Theory and Practice » On the First Law of Causal Inference — November 29, 2014 @ 4:09 am
lustra na wymiar piotrków
See this lustra na wymiar for yourself.Glass furniture,building and much more in Piotrków Trybunalski
Trackback by lustra — May 7, 2015 @ 7:12 am