Causal Analysis in Theory and Practice

From Melanie Wall, University of Minnesota:

I am teaching a course in latent variable modeling (to biostatistics and other public health students) and was yesterday introducing path analysis concepts including direct and indirect effects.

I showed them how to calculate indirect effects by taking the product of direct paths. Then a student asked about how to interpret the indirect effect and I gave the answer that I always give, that the indirect effect ab (in the following simple model) is the effect that a change in x has on Z through its relationship with Y.

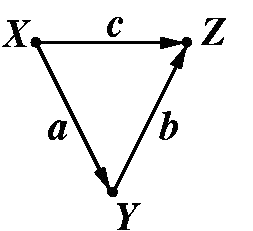
After chewing on this for a second, the student asked the following:

Student: "The interpretation of the b path is: b is the increase we would see in Z given a unit increase in Y while holding X fixed, right?"

Me: "That's right"

Student: "Then what is being held constant when we interpret an indirect effect?"

Me: "Not sure what you mean"

Student: "You said the interpretation of the indirect effect ab is: ab is the increase we would see in Z given a one unit increase in X through its causal effect on Y. But since b (the direct effect from Y to Z) requires X to be held constant how can it be used in a calculation that is also requiring X to change one unit"

Me: "Hmm. Very good question, I'm not sure I have a good answer for you. In the case where the direct path from X Z is zero I think we have no problem since the relationship between Y and Z then has nothing to do with X. But you are right, here if "c" is non-zero then we must interpret b as the effect of Y on Z when X is held constant. I understand that this sounds like it conflicts with the interpretation of the ab indirect effect where we are examining what a change in X will cause. How about I get back to you. As I have told you before, the calculations here aren't hard, its trying to truly understand what your model means that's hard."