Reversing Statistical Time
From Keith A. Markus, John Jay College of Criminal Justice, CUNY
Can you provide a general method for solving for the parameters a, b, c, and d, to achieve the exact reversal of the alignment of physical and statistical time? In other words, what is the general principle behind the example on page 59 for selecting the alternative coordinate system that will have the intended effect?
Consider any two time-dependent variables X(t) and Y(t). These may represent the position of two particles in one dimension, temperature and pressure, sales and advertising-budget, or whatever.
Assume that temporal variation of X(t) and Y(t) is governed by the equations:
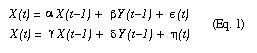
with e(t) and h(t) being mutually and serially uncorrelated noise terms.
In this coordinate system, we find that the two components of the current state, X(t) and Y(t), are uncorrelated conditioned on the components of the previous state, X(t-1) and Y(t-1). Simultaneously, the components of the current state, X(t) and Y(t), are CORRELATED conditioned on the component of the future state X(t+1) and Y(t+1). Thus, according to Definition 2.8.1 (page 58), the statistical time coincides with the physical time.
Now let us rotate the coordinates using the transformation
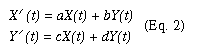
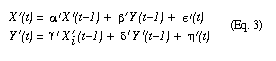
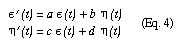
The governing physical equations remain the same as Eq. (1) but, written in the new coordinate system, they read
The primed coefficients can be obtained from the original (unprimed) coefficients by matrix multiplication. Likewise, we have:
Since e(t) and h(t) are uncorrelated, e'(t) and h'(t) will be correlated, and we no longer have the condition that the components of the current state, X'(t) and Y'(t), are uncorrelated conditioned on the components of the previous state, X'(t-1) and Y'(t-1). Thus, the statistical time (if there is one) no longer runs along the physical time.
Now we need to show that we can choose the parameters a, b, c and d in such a way as to have the statistical time run opposite to the physical time, namely, to make the components of the current state, X'(t) and Y'(t), uncorrelated conditioned on the components of the future state, X'(t+1) and Y'(t+1).
By inverting Eq.(3) we can express X'(t-1) and Y'(t-1) in terms of linear combinations of X'(t), Y'(t), e'(t) and h'(t). Clearly, since e(t) and h(t) are uncorrelated, we can choose a,b,c,d in such a way that the noise term appearing in the X'(t-1) equation is uncorrelated with the one appearing in the Y'(t-1) equation. (This is better demonstrated in matrix calculus).
Thus, the general principle for selecting the alternative coordinate system is to diagonalize the noise correlation matrix in the reverse direction.
Thanks for your interest in this problem; I hope you or some other readers undertake the challenge of testing the Temporal Bias Conjecture (page 59):
" In most natural phenomenon, the physical time
coincides with at least one statistical time."
My former student, Alex Balke, tried to test it with economical time series, but the results were not too conclusive, for lack of adequate data. I still believe in the truth of the conjecture, and I hope readers will have better luck.
Best wishes,
========Judea Pearl
Comment by judea — May 11, 2000 @ 12:00 pm