Scott Mueller and Judea Pearl
Abstract
Personalized decision making targets the behavior of a specific individual, while population-based decision making concerns a sub-population resembling that individual. This paper clarifies the distinction between the two and explains why the former leads to more informed decisions. We further show that by combining experimental and observational studies we can obtain valuable information about individual behavior and, consequently, improve decisions over those obtained from experimental studies alone.
Introduction
The purpose of this paper is to provide a conceptual understanding of the distinction between personalized and population-based decision making, and to demonstrate both the advantages of the former and how it could be achieved.
Formally, this distinction is captured in the following two causal effects. Personalized decision making optimizes the Individual Causal Effect (ICE):
$$\begin{equation}
\text{ICE}(u) = Y(1,u)-Y(0,u)
\end{equation}$$
where \(Y(x,u)\) stands for the outcome that individual \(u\) would attain had decision \(x \in \{1, 0\}\) been taken. In contrast, population-based decision making optimizes the Conditional Average Causal Effect (CACE):
$$\begin{equation}
\text{CACE}(u) = E[Y(1,u’) – Y(0,u’) | C(u’) = C(u)]
\end{equation}$$
where \(C(u)\) stands for a vector of characteristics observed on individual \(u\), and the average is taken over all units \(u’\) that share these characteristics.
We will show in this paper that the two objective functions lead to different decision strategies and that, although \(\text{ICE}(u)\) is in general not identifiable, informative bounds can nevertheless be obtained by combining experimental and observational studies. We will further demonstrate how these bounds can improve decisions that would otherwise be taken using \(\text{CACE}(u)\) as an objective function.
The paper is organized as follows. Section 2 will demonstrate, using an extreme example, two rather surprising findings. First, that population data are capable of providing decisive information on individual response and, second, that non-experimental data, usually discarded as bias-prone, can add information (regarding individual response) beyond that provided by a Randomized Controlled Trial (RCT) alone. Section 3 will generalize these findings using a more realistic example, and will further demonstrate how critical decisions can be made using the information obtained and their ramifications to both the targeted individual and to a population-minded policy maker. Section 4 casts the findings of Section 3 in a numerical setting, allowing for a quantitative appreciation of the magnitudes involved. This analysis leads to actionable policies that guarantee risk-free benefits in certain populations.
Preliminary Semi-qualitative Example
Our target of analysis is an individual response to a given treatment, namely, how an individual would react if given treatment and if denied treatment. Since no individual can be subjected to both treatment and its denial, its response function must be inferred from population data, originating from one or several studies. We are asking therefore: to what degree can population data inform us about an individual response?
Before tackling this general question, we wish to address two conceptual hurdles. First, why should population data provide any information whatsoever on the individual response and, second, why should non-experimental data add any information (regarding individual response) to what we can learn with an RCT alone. The next simple example will demonstrate both points.
We conduct an RCT and find no difference between treatment (drug) and control (placebo), say \(10\%\) in both treatment and control groups die, while the rest (\(90\%\)) survive. This makes us conclude that the drug is ineffective, but also leaves us uncertain between (at least) two competing models:
- Model-1 — The drug has no effect whatsoever on any individual and
- Model-2 — The drug saves \(10\%\) of the population and kills another \(10\%\).
From a policy maker viewpoint the two models may be deemed equivalent, the drug has zero average effect on the target population. But from an individual viewpoint the two models differ substantially in the sets of risks and opportunities they offer. According to Model-1, the drug is useless but safe. According to Model-2, however, the drug may be deemed dangerous by some and a life-saver by others.
To see how such attitudes may emerge, assume, for the sake of argument, that the drug also provides temporary pain relief. Model-1 would be deemed desirable and safe by all, whereas Model-2 will scare away those who do not urgently need the pain relief, while offering a glimpse of hope to those whose suffering has become unbearable, and who would be ready to risk death for the chance (\(10\%\)) of recovery. (Hoping, of course, they are among the lucky beneficiaries.)
This simple example will also allow us to illustrate the second theme of our paper – the crucial role of observational studies. We will now show that supplementing the RCT with an observational study on the same population (conducted, for example, by an independent survey of patients who have the option of taking or avoiding the drug) would allow us to decide between the two models, totally changing our understanding of what risks await an individual taking the drug.
Consider an extreme case where the observational study shows \(100\%\) survival in both drug-choosing and drug-avoiding patients, as if each patient knew in advance where danger lies and managed to avoid it. Such a finding, though extreme and unlikely, immediately rules out Model-1 which claims no treatment effect on any individual. This is because the mere fact that patients succeed \(100\%\) of the time to avoid harm where harm does exist (revealed through the \(10\%\) death in the randomized trial) means that choice makes a difference, contrary to Model-1’s claim that choice makes no difference.
The reader will surely see that the same argument applies when the probability of survival among option-having individuals is not precisely \(100\%\) but simply higher (or lower) than the probability of survival in the RCT. Using the RCT study alone, in contrast, we were unable to rule out Model-1, or even to distinguish Model-1 from Model-2.
We now present another edge case where Model-2, rather than Model-1, is ruled out as impossible. Assume the observational study informs us that all those who chose the drug died and all who avoided the drug survived. It seems that drug-choosers were truly dumb while drug-avoiders knew precisely what’s good for them. This is perfectly feasible, but it also tells us that no one can be cured by the drug, contrary to the assertion made by Model-2, that the drug cures \(10\%\) and kills \(10\%\). To be cured, a person must survive if treated and die if not treated. But none of the drug-choosers were cured, because they all died, and none of the drug avoiders were cured because they all survived. Thus, Model-2 cannot explain these observational results, and must be ruled out.
Now that we have demonstrated conceptually how certain combinations of observational and experimental data can provide information on individual behavior that each study alone cannot, we are ready to go to a more realistic motivating example which, based on theoretical bounds derived in Tian and Pearl, 2000, establishes individual behavior for any combination of observational and experimental data and, moreover, demonstrates critical decision making ramifications of the information obtained.
Footnote
Motivating Numerical Example
The next example to be considered deals with the effect of a drug on two subpopulations, males and females. Unlike the extreme case considered in Section 2, the drug is found to be somewhat effective for both males and females and, in addition, deaths are found to occur in the observational study as well.
To cast the story in a realistic setting, we imagine the testing of a new drug, aimed to help patients suffering from a deadly disease. An RCT is conducted to evaluate the efficacy of the drug and is found to be \(28\%\) effective in both males and females. In other words \(\text{CACE}(\text{male}) = \text{CACE}(\text{female}) = 0.28\). The drug is approved and, after a year of use, a follow up randomized study is conducted yielding the same results; namely CACE remained 0.28, and men and women remained totally indistinguishable in their responses, as shown in Table 1.
|
Experimental |
|
\(do(\text{drug})\) |
\(do(\text{no drug})\) |
\(\text{CACE}\) |
| Female Survivals |
489/1000 (49%) |
210/1000 (21%) |
28% |
| Male Survivals |
490/1000 (49%) |
210/1000 (21%) |
28% |
Table 1: Female vs male CACE
|
Female Data |
|
Experimental |
Observational |
|
\(do(\text{drug})\) |
\(do(\text{no drug})\) |
\(\text{drug}\) |
\(\text{no drug}\) |
| Survivals |
489 (49%) |
210 (21%) |
378 (27%) |
420 (70%) |
| Deaths |
511 (51%) |
790 (79%) |
1,022 (73%) |
180 (30%) |
| Total |
1,000 (50%) |
1,000 (50%) |
1,400 (70%) |
600 (30%) |
Table 2: Female survival and recovery data
|
Male Data |
|
Experimental |
Observational |
|
\(do(\text{drug})\) |
\(do(\text{no drug})\) |
\(\text{drug}\) |
\(\text{no drug}\) |
| Survivals |
490 (49%) |
210 (21%) |
980 (70%) |
420 (70%) |
| Deaths |
510 (51%) |
790 (79%) |
420 (30%) |
180 (30%) |
| Total |
1,000 (50%) |
1,000 (50%) |
1,400 (70%) |
600 (30%) |
Table 3: Male survival and recovery data
Let us focus on the second RCT (Table 1), since the first was used for drug approval only, and its findings are the same as the second. The RCT tells us that there was a \(28\%\) improvement, on average, in taking the drug compared to not taking the drug. This was the case among both females and males: \(\text{CACE}(\text{female}) = \text{CACE}(\text{male}) = 0.28\), where \(do(\text{drug})\) and \(do(\text{no-drug})\) are the treatment and control arms in the RCT. It thus appears reasonable to conclude that the drug has a net remedial effect on some patients and that every patient, be it male or female, should be advised to take the drug and benefit from its promise of increasing one’s chances of recovery (by \(28\%\)).
At this point, the drug manufacturer ventured to find out to what degree people actually buy the approved drug, following its recommended usage. A market survey was conducted (observational study) and revealed that only \(70\%\) of men and \(70\%\) of women actually chose to take the drug; problems with side effects and rumors of unexpected deaths may have caused the other \(30\%\) to avoid it. A careful examination of the observational study has further revealed substantial differences in survival rates of men and women who chose to use the drug (shown in Tables 2 and 3). The rate of recovery among drug-choosing men was exactly the same as that among the drug-avoiding men (\(70\%\) for each), but the rate of recovery among drug-choosing women was \(43\%\) lower than among drug-avoiding women (\(0.27\) vs \(0.70\), in Table 2). It appears as though many women who chose the drug were already in an advanced stage of the disease, which may account for their low recovery rate of \(27\%\).
At this point, having data from both experimental and observational studies we can estimate the individual treatment effects for both a typical man and a typical woman. Quantitative analysis shows (see Section 4) that, with the data above, the drug affects men markedly differently from the way it affects women. Whereas a woman has a \(28\%\) chance of benefiting from the drug and no danger at all of being harmed by it, a man has a \(49\%\) chance of benefiting from it and as much as a \(21\%\) chance of dying because of it — a serious cause for concern. Note that based on the experimental data alone (Table 1), no difference at all can be noticed between men and women.
The ramifications of these findings on personal decision making are enormous. First, they tell us that the drug is not as safe as the RCT would have us believe, it may cause death in a sizable fraction of patients. Second, they tell us that a woman is totally clear of such dangers, and should have no hesitation to take the drug, unlike a man, who faces a decision; a \(21\%\) chance of being harmed by the drug is cause for concern. Physicians, likewise, should be aware of the risks involved before recommending the drug to a man. Third, the data tell policy makers what the overall societal benefit would be if the drug is administered to women only; \(28\%\) of the drug-takers would survive who would die otherwise. Finally, knowing the relative sizes of the benefiting vs harmed subpopulations swings open the door for finding the mechanisms responsible for the differences as well as identifying measurable markers that characterize those subpopulations.
For example:
- In the same way that our analysis has identified “Sex” to be an important feature, separating those who are harmed from those saved by the drug, so we can leverage other measured features, say family history, a genetic marker, or a side-effect, and check whether they shrink the sizes of the susceptible subpopulations. The results would be a set of features that approximate responses at the individual level. Note again that absent observational data and a calculus for combining them with the RCT data, we would not be able to identify such informative features. A feature like “Sex” would be deemed irrelevant, since men and women were indistinguishable in our RCT studies.
- Our ability to identify relevant informative features as described above can be leveraged to amplify the potential benefits of the drug. For example, if we identify a marker that characterizes men who would die only if they take the drug and prevent those patients from taking the drug, the drug would cure \(62\%\) of male patients who would be allowed to use it. This is because we don’t administer the drug to the \(21\%\) who would’ve been killed by the drug. Those patients will now survive, so a total of \(70\%\) of patients will be cured because of this combination of marker identification and drug administration. This unveils an enormous potential of the drug at hand, which was totally concealed by the \(28\%\) effectiveness estimated in the RCT studies.
How the Results Were Obtained
For the purpose of analysis, let us denote \(y_t\) as recovery among the RCT treatment group and \(y_c\) as recovery among the RCT control group. The causal effects for treatment and control groups, \(P(y_t|\text{Gender})\) and \(P(y_c|\text{Gender})\), were the same, no differences were noted between males and females.
In addition to the above RCT, we posited an observational study (survey) conducted on the same population. Let us denote \(P(y|t, \text{Gender})\) and \(P(y|c, \text{Gender})\) as recovery among the drug-choosers and recovery among the drug-avoiders, respectively.
With this notation at hand, our problem is to compute the probability of benefit
$$\begin{equation}
P(\text{benefit}) = P(y_t, y’_c)
\end{equation}$$
from the following data sources: \(P(y_t)\), \(P(y_c)\), \(P(y|t)\), \(P(y|c)\), and \(P(t)\). The first two denote the data obtained from the RCT and the last three, data obtained from the survey. Eq. (3) should be interpreted as the probability that an individual would both recover if assigned to the RCT treatment arm and die if assigned to control.
Connecting the experimental and observational data is an important assumption known as consistency (Pearl, 2009, 2010). In other words, we assume that the units selected for an observational or experimental study are drawn from the same population and that their response to treatment is purely biological, unaffected by their respective settings.
In other words, the outcome of a person choosing the drug would be the same had this person been assigned to the treatment group in an RCT study. Similarly, if we observe someone avoiding the drug, their outcome is the same as if they were in the control group of our RCT. Deviation from consistency, normally attributed to uncontrolled “placebo effects”, should be dealt with by explicitly representing such factors in the model.
In terms of our notation, consistency implies:
$$\begin{equation}
P(y_t|t)= P(y|t), P(y_c|c)= P(y|c).
\end{equation}$$
In words, the probability that a drug-chooser would recover in the treatment arm of the RCT, \(P(y_t|t)\), is the same as the probability of recovery in the observational study, \(P(y|t)\).
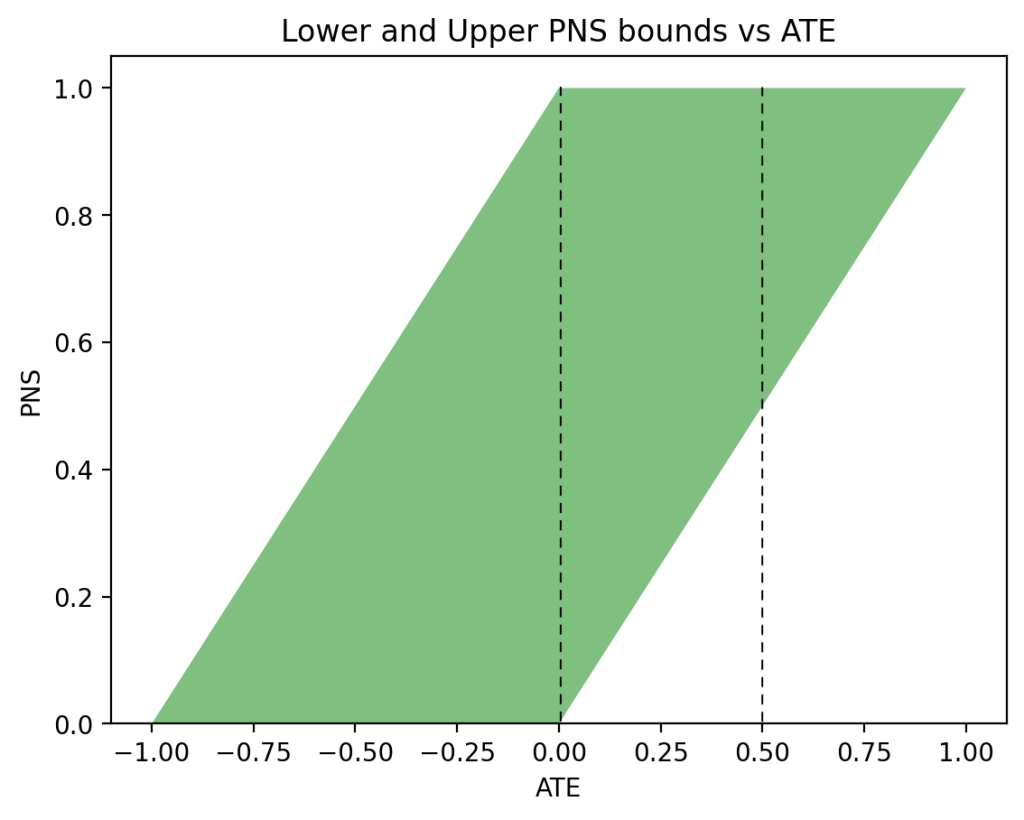
Based on this assumption, and leveraging both experimental and observational data, Tian and Pearl (Tian and Pearl, 2000) derived the following tight bounds on the probability of benefit, as defined in (3):
$$\begin{equation}
\max\left\{\begin{array}{c}
0,\\
P(y_t) – P(y_c),\\
P(y) – P(y_c),\\
P(y_t) – P(y)\\
\end{array}\right\} \leqslant P(\text{benefit}) \leqslant \min\left\{\begin{array}{c}
P(y_t),\\
P(y’_c),\\
P(t,y) + P(c,y’),\\
P(y_t) – P(y_c)\ +\\
\ P(t, y’) + P(c, y)
\end{array}\right\}.
\end{equation}$$
Here \(P(y’_c)\) stands for \(1-P(y_c)\), namely the probability of death in the control group. The same bounds hold for any subpopulation, say males or females, if every term in (5) is conditioned on the appropriate class.
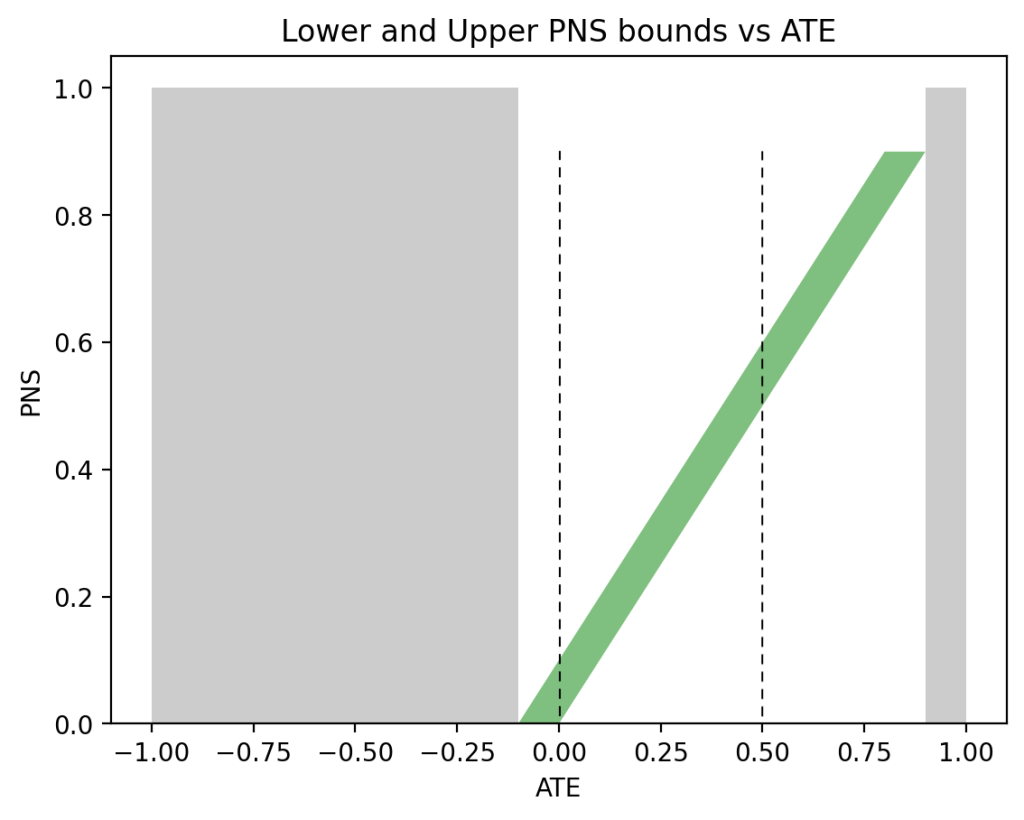
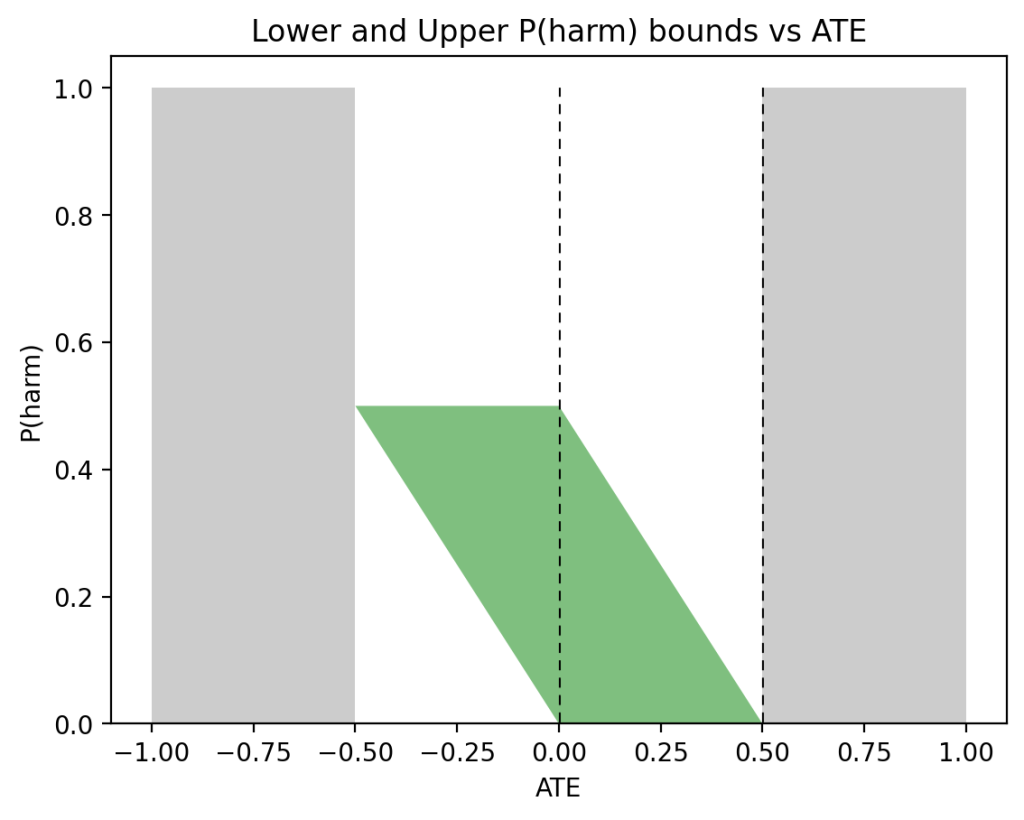
Applying these expressions to the female data from Table 2 gives the following bounds on \(P(\text{benefit}|\text{female})\):
$$\begin{align}
\max\{0, 0.279, 0.09, 0.189\} &\leqslant P(\text{benefit}|\text{female}) \leqslant \min\{0.489,0.79,0.279,1\},\nonumber\\
0.279 &\leqslant P(\text{benefit}|\text{female}) \leqslant 0.279.
\end{align}$$
Similarly, for men we get:
$$\begin{align}
\max\{0, 0.28, 0.49, -0.21\} &\leqslant P(\text{benefit}|\text{male}) \leqslant \min\{0.49, 0.79, 0.58, 0.7\},\nonumber\\
0.49 &\leqslant P(\text{benefit}|\text{male}) \leqslant 0.49.
\end{align}$$
Thus, the bounds for both females and males, in (6) and (7), collapse to point estimates:
$$\begin{align*}
P(\text{benefit}|\text{female}) &= 0.279,\\
P(\text{benefit}|\text{male}) &= 0.49.
\end{align*}$$
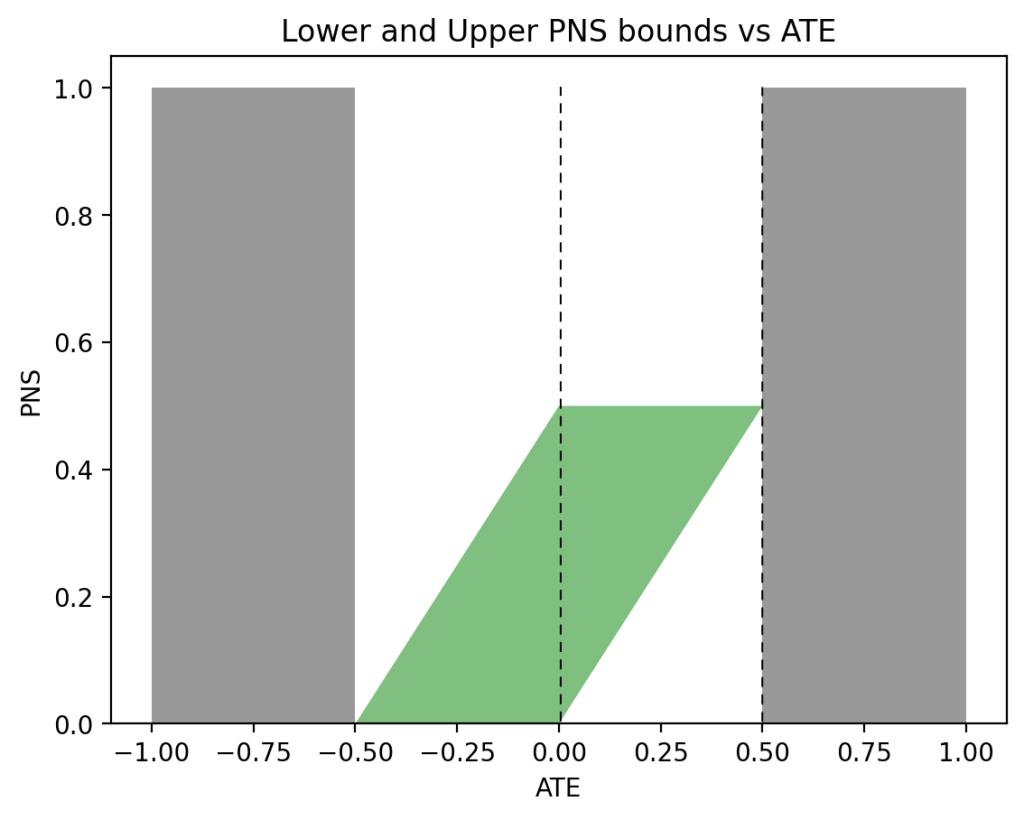
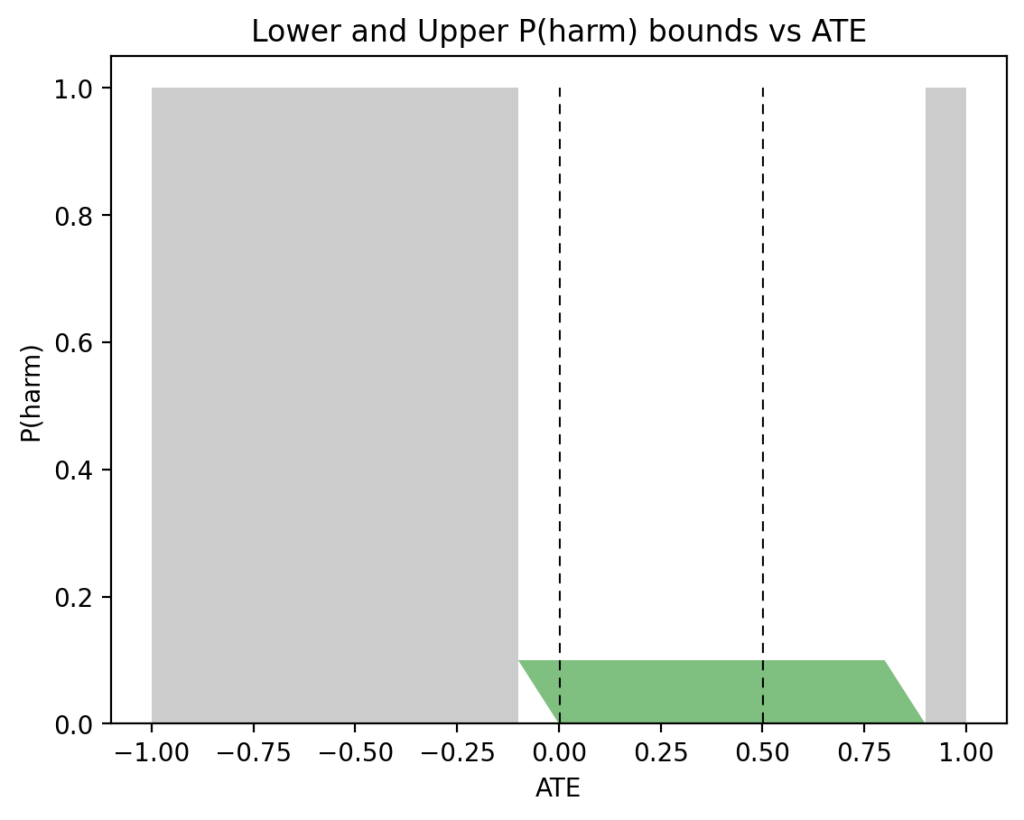
We aren’t always so fortunate to have a complete set of observational and experimental data at our disposal. When some data is absent, we are allowed to discard arguments to \(\max\) or \(\min\) in (5) that depend on that data. For example, if we lack all experimental data, the only applicable lower bound in (5) is \(0\) and the only applicable upper bound is \(P(t, y) + P(c, y’)\):
$$\begin{equation}
0 \leqslant P(\text{benefit}) \leqslant P(t, y) + P(c, y’).
\end{equation}$$
Applying these observational data only bounds to males and females yields:
$$\begin{align*}
0 &\leqslant P(\text{benefit}|\text{female}) \leqslant 0.279,\\
0 &\leqslant P(\text{benefit}|\text{male}) \leqslant 0.58.
\end{align*}$$
Naturally, these are far more loose than the point estimates when combined experimental and observational data is fully available. Let’s similarly examine what can be computed with purely experimental data. Without observational data, only the first two arguments to \(\max\) of the lower bound and \(\min\) of the upper bound of \(P(\text{benefit})\) in (5) are applicable:
$$\begin{equation}
\max\{0,P(y_t)-P(y_c)\} \leqslant P(\text{benefit}) \leqslant \min\{P(y_t),P(y’_c)\}.
\end{equation}$$
Applying these experimental data only bounds to males and females yields:
$$\begin{align*}
0.279 &\leqslant P(\text{benefit}|\text{female}) \leqslant 0.489,\\
0.28 &\leqslant P(\text{benefit}|\text{male}) \leqslant 0.49.
\end{align*}$$
Again, these are fairly loose bounds, especially when compared to the point estimates obtained with combined data. Notice that the overlap between the female bounds using observational data, \(0 \leqslant P(\text{benefit}|\text{female}) \leqslant 0.279\), and the female bounds using experimental data, \(0.279 \leqslant P(\text{benefit}|\text{female}) \leqslant 0.489\) is the point estimate \(P(\text{benefit}|\text{female}) = 0.279\). The more comprehensive Tian-Pearl bounds formula (5) wasn’t necessary. However, the intersection of the male bounds using observational data, \(0 \leqslant P(\text{benefit}|\text{male}) \leqslant 0.58\), and the male bounds using experimental data, \(0.28 \leqslant P(\text{benefit}|\text{male}) \leqslant 0.49\), does not provide us with narrower bounds. For males, the comprehensive Tian-Pearl bounds in (5) was necessary for narrow bounds (in this case, a point estimate).
Having seen this mechanism of combining observational and experimental data in (5) work so well, the reader may ask what’s behind this? The intuition comes from the fact that observational data incorporates individuals’ whims. Whimsy is a proxy for much deeper behavior. This leads to confounding, which is ordinarily problematic for causal inference and leads to spurious conclusions, sometimes completely reversing a treatment’s effect (Pearl, 2014). Confounding then needs to be adjusted for. However, here confounding helps us, exposing the underlying mechanisms its associated whims and desires are a proxy for.
Finally, as noted in Section 3, knowing the relative sizes of the benefiting vs harmed subpopulations demands investment in finding mechanisms responsible for the differences as well as characterizations of those subpopulations. For example, women above a certain age may be affected differently by the drug, to be detected by how age affects the bounds on the individual response. Such characteristics can potentially be narrowed repeatedly until the drug’s efficacy can be predicted for an individual with certainty or the underlying mechanisms of the drug can be fully understood.
None of this was possible with only the RCT. Yet, remarkably, an observational study, however sloppy and uncontrolled, provides a deeper perspective on a treatment’s effectiveness. It incorporates individuals’ whims and desires that govern behavior under free-choice settings. And, since such whims and desires are often proxies for factors that also affect outcomes and treatments (i.e., confounders), we gain additional insight hidden by RCTs.
Footnote
Annotated Bibliography for Related Works
The following is a list of papers that analyze probabilities of causation and lead to the results reported above.
- Chapter 9 of Causality (Pearl, 2009) derives bounds on individual-level probabilities of causation and discusses their ramifications in legal settings. It also demonstrates how the bounds collapse to point estimates under certain combinations of observational and experimental data.
- (Tian and Pearl, 2000) develops bounds on individual level causation by combining data from experimental and observational studies. This includes Probability of Sufficiency (PS), Probability of Necessity (PN), and Probability of Necessity and Sufficiency (PNS). PNS is equivalent to \(P(\text{benefit})\) above. \(\text{PNS}(u) = P(\text{benefit}|u)\), the probability that individual \(U=u\) survives if treated and does not survive if not treated, is related to \(\text{ICE}(u)\) (1) via the equation:
$$\begin{equation}
\text{PNS}(u) = P(\text{ICE}(u’) > 0 | C(u’) = C(u)).
\end{equation}$$
In words, \(\text{PNS}(u)\) equals the proportion of units \(u’\) sharing the characteristics of \(u\) that would positively benefit from the treatment. The reason is as follows. Recall that (for binary variables) \(\text{ICE}(u)\) is \(1\) when the individual benefits from the treatment, \(\text{ICE}(u)\) is \(0\) when the individual responds the same to either treatment, and \(\text{ICE}(u)\) is \(-1\) when the individual is harmed by treatment. Thus, for any given population, \(\text{PNS} = P(\text{ICE}(u) > 0)\). Focusing on the sub-population of individuals \(u’\) that share the characteristics of \(u\), \(C(u’) = C(u)\), we obtain (10). In words, \(\text{PNS}(u)\) is the fraction of indistinguishable individuals that would benefit from treatment. Note that whereas (2) is can be estimated by controlled experiments over the population \(C(u’)=C(u)\), (10) is defined counterfactually, hence, it cannot be estimated solely by such experiments; it requires additional ingredients as described in the text below.
- (Mueller and Pearl, 2020) provides an interactive visualization of individual level causation, allowing readers to observe the dynamics of the bounds as one changes the available data.
- (Li and Pearl, 2019) optimizes societal benefit of selecting a unit \(u\), when provided costs associated with the four different types of individuals, benefiting, harmed, always surviving, and doomed.
- (Mueller et al., 2021) takes into account the causal graph to obtain narrower bounds on PNS. The hypothetical study in this article was able to calculate point estimates of PNS, but often the best we can get are bounds.
- (Pearl, 2015) demonstrates how combining observational and experimental data can be informative for determining Causes of Effects, namely, assessing the probability PN that one event was a necessary cause of an observed outcome.
- (Dawid and Musio, 2022) analyze Causes of Effects (CoE), defined by PN, the probability that a given intervention is a necessary cause for an observed outcome. Dawid and Musio further analyze whether bounds on PN can be narrowed with data on mediators.
Conclusion
One of the least disputed mantra of causal inference is that we cannot access individual causal effects; we can observe an individual response to treatment or to no-treatment but never to both. However, our theoretical results show that we can get bounds on individual causal effects, which sometimes can be quite narrow and allow us to make accurate personalized decisions. We project therefore that these theoretical results are key for next-generation personalized decision making.
References
- Dawid, A. P., & Musio, M. (2022). Effects of causes and causes of effects. Annual Review of Statistics and its Application. https://arxiv.org/pdf/2104.00119.pdf
- Li, A., & Pearl, J. (2019). Unit selection based on counterfactual logic. Proceedings of the 28th International Joint Conference on Artificial Intelligence, 1793-1799.
- Mueller, S., Li, A., & Pearl, J. (2021). Causes of effects: Learning individual responses from population data. http://ftp.cs.ucla.edu/pub/statser/r505.pdf
- Mueller, S., & Pearl, J. (2020). Which Patients are in Greater Need: A counterfactual analysis with reflections on COVID-19 [https://ucla.in/39Ey8sU+].
- Pearl, J. (2009). Causality (Second). Cambridge University Press.
- Pearl, J. (2010). On the consistency rule in causal inference: An axiom, definition, assumption, or a theorem? Epidemiology, 21(6), 872-875. https://ftp.cs.ucla.edu/pub/stat_ser/r358-reprint.pdf
- Pearl, J. (2014). Understanding simpson’s paradox. The American Statistician, 68(1), 8-13. http://ftp.cs.ucla.edu/pub/stat_ser/r414-reprint.pdf
- Pearl, J. (2015). Causes of effects and effects of causes. Journal of Sociological Methods and Research, 44(1), 149-164. http://ftp.cs.ucla.edu/pub/stat_ser/r431-reprint.pdf
- Rubin, D. B. (1974). Estimating causal effects of treatments in randomized andnonrandomized studies. Journal of Educational Psychology, 66(5), 688-701. https://doi.org/10.1037/h0037350
- Tian, J., & Pearl, J. (2000). Probabilities of causation: Bounds and identification. Annals of Mathematics and Artificial Intelligence, 28(1-4), 287-313. http://ftp.cs.ucla.edu/pub/stat_ser/r271-A.pdf
]]>